题目内容
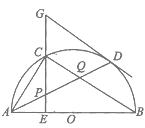
【题目】如图,在⊙O中,AB是直径,点D是⊙O上一点,点C是![]() 的中点,弦CE⊥AB于点E,过点D的切线交EC的延长线于点G,连接AD,分别交CF、BC于点P、Q,连接AC.给出下列结论:
的中点,弦CE⊥AB于点E,过点D的切线交EC的延长线于点G,连接AD,分别交CF、BC于点P、Q,连接AC.给出下列结论:
①∠BAD=∠ABC;②GP=GD;③点P是△ACQ的外心.
其中正确结论是________ (只需填写序号).
【答案】②③.
【解析】
试题分析:∠BAD与∠ABC不一定相等,选项①错误;
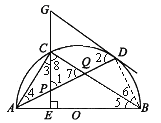
∵GD为圆O的切线,∴∠GDP=∠ABD,又AB为圆O的直径,∴∠ADB=90°,∵CF⊥AB,∴∠AEP=90°,∴∠ADB=∠AEP,又∠PAE=∠BAD,∴△APE∽△ABD,∴∠ABD=∠APE,又∠APE=∠GPD,∴∠GDP=∠GPD,∴GP=GD,选项②正确;
由AB是直径,则∠ACQ=90°,如果能说明P是斜边AQ的中点,那么P也就是这个直角三角形外接圆的圆心了.Rt△BQD中,∠BQD=90°-∠6, Rt△BCE中,∠8=90°-∠5,而∠7=∠BQD,∠6=∠5, 所以∠8=∠7, 所以CP=QP;由②知:∠3=∠5=∠4,则AP=CP; 所以AP=CP=QP,则点P是△ACQ的外心,选项③正确.
则正确的选项序号有②③.故答案为:②③.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案【题目】某校师生为了对学生零花钱的使用进行教育指导,对全班50名学生每人一周内的零花钱数额进行了调查统计,并绘制如下统计表:
零花钱数额/元 | 5 | 10 | 15 | 20 |
学生人数/名 | a | 15 | 20 | 5 |
根据表格中信息,回答下列问题:
(1)求a的值.
(2)求着50名学生每人一周内零花钱数额的中位数.
(3)随机抽查一名学生,抽到一周内零花钱数额不大于10元的同学概率为多少?
【题目】甲、乙两班举行电脑汉字输入比赛,参赛学生每分钟输入汉字的个数统计结果如下表:
班级 | 参赛人数 | 中位数 | 方差 | 平均数 |
甲 | 55 | 149 | 191 | 135 |
乙 | 55 | 151 | 110 | 135 |
某同学分析上表后得出如下结论:
①甲、乙两班学生成绩平均水平相同;
②乙班优秀的人数多于甲班优秀的人数(每分钟输入汉字≥150个为优秀);
③甲班成绩的波动比乙班大,
上述结论正确的是( )
A.①②③
B.①②
C.①③
D.②③