Question

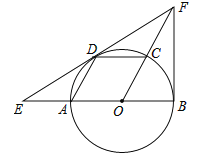
【题目】如图，AB是⊙O的直径，点C、D在圆上，且四边形AOCD是平行四边形，过点D作⊙O的切线，分别交OA延长线与OC延长线于点E、F，连接BF．

（1）求证：BF是⊙O的切线；

（2）已知圆的半径为1，求EF的长．

Answer 1

【答案】（1）证明见解析；（2）．

【解析】

试题分析：（1）先证明四边形AOCD是菱形，从而得到∠AOD=∠COD=60°，再根据切线的性质得∠FDO=90°，接着证明△FDO≌△FBO得到∠ODF=∠OBF=90°，然后根据切线的判定定理即可得到结论；

（2）在Rt△OBF中，利用60度的正切的定义求解．

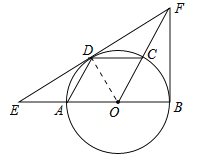
试题解析：（1）证明：连结OD，如图，∵四边形AOCD是平行四边形，而OA=OC，∴四边形AOCD是菱形，∴△OAD和△OCD都是等边三角形，∴∠AOD=∠COD=60°，∴∠FOB=60°，∵EF为切线，∴OD⊥EF，∴∠FDO=90°，在△FDO和△FBO中，∵OD=OB，∠FOD=∠FOB，FO=FO，∴△FDO≌△FBO，∴∠ODF=∠OBF=90°，∴OB⊥BF，∴BF是⊙O的切线；

（2）解：在Rt△OBF中，∵∠FOB=60°，而tan∠FOB=，∴BF=1×tan60°=．∵∠E=30°，∴EF=2BF=．