Question

【题目】如图，n个边长为1的相邻正方形的一边均在同一直线上，点M1 ， M2 ， M3 ， …Mn分别为边B1B2 ， B2B3 ， B3B4 ， …，BnBn+1的中点，△B1C1M1的面积为S1 ， △B2C2M2的面积为S2 ， …△BnCnMn的面积为Sn ， 则Sn= ． （用含n的式子表示）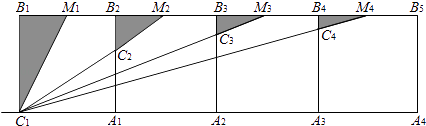

Answer 1

【答案】
【解析】解：∵n个边长为1的相邻正方形的一边均在同一直线上，点M1 ， M2 ， M3 ， …Mn分别为边B1B2 ， B2B3 ， B3B4 ， …，BnBn+1的中点， ∴S1= ×B1C1×B1M1= ×1× = ，
S△B1C1M2= ×B1C1×B1M2= ×1× = ，
S△B1C1M3= ×B1C1×B1M3= ×1× = ，
S△B1C1M4= ×B1C1×B1M4= ×1× = ，
S△B1C1Mn= ×B1C1×B1Mn= ×1× = ，
∵BnCn∥B1C1 ，
∴△BnCnMn∽△B1C1Mn ，
∴S△BnCnMn：S△B1C1Mn=（ ）2=（ ）2 ，
即Sn： = ，
∴Sn= ．
故答案为： ．
由n个边长为1的相邻正方形的一边均在同一直线上，点M1 ， M2 ， M3 ， …Mn分别为边B1B2 ， B2B3 ， B3B4 ， …，BnBn+1的中点，即可求得△B1C1Mn的面积，又由BnCn∥B1C1 ， 即可得△BnCnMn∽△B1C1Mn ， 然后利用相似三角形的面积比等于相似比的平方，求得答案．