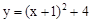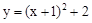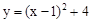题目内容
如图1,在等腰△ABC中,底边BC=8,高AD=2,一动点Q从B点出发,以每秒1个单位的速度沿BC向右运动,到达D点停止;另一动点P从距离B点1个单位的位置出发,以相同的速度沿BC向右运动,到达DC中点停止;已知P、Q同时出发,以PQ为边作正方形PQMN,使正方形PQMN和△ABC在BC的同侧,设运动的时间为t秒(t≥0).
(1)当点N落在AB边上时,t的值为 ,当点N落在AC边上时,t的值为 ;
(2)设正方形PQMN与△ABC重叠部分面积为S,求出当重叠部分为五边形时S与t的函数关系式以及t的取值范围;
(3)(本小题选做题,做对得5分,但全卷不超过150分)
如图2,分别取AB、AC的中点E、F,连接ED、FD,当点P、Q开始运动时,点G从BE中点出发,以每秒 个单位的速度沿折线BE-ED-DF向F点运动,到达F点停止运动.请问在点P的整个运动过程中,点G可能与PN边的中点重合吗?如果可能,请直接写出t的值或取值范围;若不可能,请说明理由.
个单位的速度沿折线BE-ED-DF向F点运动,到达F点停止运动.请问在点P的整个运动过程中,点G可能与PN边的中点重合吗?如果可能,请直接写出t的值或取值范围;若不可能,请说明理由.

(1)当点N落在AB边上时,t的值为 ,当点N落在AC边上时,t的值为 ;
(2)设正方形PQMN与△ABC重叠部分面积为S,求出当重叠部分为五边形时S与t的函数关系式以及t的取值范围;
(3)(本小题选做题,做对得5分,但全卷不超过150分)
如图2,分别取AB、AC的中点E、F,连接ED、FD,当点P、Q开始运动时,点G从BE中点出发,以每秒
 个单位的速度沿折线BE-ED-DF向F点运动,到达F点停止运动.请问在点P的整个运动过程中,点G可能与PN边的中点重合吗?如果可能,请直接写出t的值或取值范围;若不可能,请说明理由.
个单位的速度沿折线BE-ED-DF向F点运动,到达F点停止运动.请问在点P的整个运动过程中,点G可能与PN边的中点重合吗?如果可能,请直接写出t的值或取值范围;若不可能,请说明理由.
(1)1 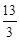
(2)
(3)可能.t=0或t=2或4≤t≤5
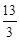
(2)

(3)可能.t=0或t=2或4≤t≤5
试题分析:本题属于学科综合题,代数知识与几何知识有机结合在一起,体现了数形结合的思想,解答此类综合题关键是数与形的灵活转化.(1)当点N落在AB边上时,NP=1,NP∥AD,利用平行线对应线段成比例的性质可算出t的值;当N落在AC边上时,正方形的边长不再是1,Q点已经停在D点,PD=t-3,∴PN="t-3," PC=4-(t-3)=7-t ∵PN∥DA ∴
 ∴
∴ ∴t=
∴t=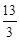 .(2)画出运动中的图形,根据具体图形利用未知数t的代数式表示并求其面积.(3)重点是准确画出图形变化,PN中点与G何时重合.
.(2)画出运动中的图形,根据具体图形利用未知数t的代数式表示并求其面积.(3)重点是准确画出图形变化,PN中点与G何时重合.试题解析: (1)解:∵NP∥AD PN=1 AD="2" ∴
 ∴PN是△ABD的中位线 ∴BP=2∴t=1
∴PN是△ABD的中位线 ∴BP=2∴t=1∵PD="t-3," ∴PN="t-3," PC=4-(t-3)=7-t
∵PN∥DA ∴
 ∴
∴ ∴t=
∴t=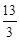 .
.( 2 )当 0<t<1,重叠部分为梯形,当1<t<2时,设EQ交AB于R,则重叠部分为五边形PQREN.

(2)当1<t<2时, 设EQ交AB于R,则重叠部分为五边形PQREN.
∵ME=2-t,MR=
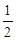 ME=
ME=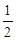 (2-t)∴S△MRE =
(2-t)∴S△MRE =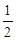 ME·MR=
ME·MR= (2-t)2
(2-t)2∴S=S正方形PQMN-S△MRE =1-
 (2-t)2=-
(2-t)2=- t2+t
t2+t 
当
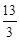 <t<5时
<t<5时设MN交AC于S,PN交AC于T,则重叠部分为五边形PQMST
∵AM=2-(t-3)=5-t,MS=2AM=2(5-t) PC=7-t,PT=
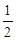 PC=
PC=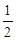 (7-t)
(7-t)∴S△AMS =
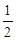 AM·MS=(5-t)2,S△PTC =
AM·MS=(5-t)2,S△PTC =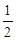 PC·PT=
PC·PT= (7-t)2
(7-t)2又S△ADC =
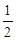 AD·CD=
AD·CD=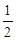 ×2×4=4
×2×4=4∴S=S△ADC-S△AMS -S△PTC =4-(5-t)2-
 (7-t)2=-
(7-t)2=- t2+
t2+ t-
t-
综上所述,当重叠部分为五边形时S与t的函数关系式为:

(3)可能. t=0或t=2或4≤t≤5
当t=0时,QP=1,GP=
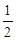 ,G为BE中点,也为NP中点.
,G为BE中点,也为NP中点.
当t=2时,G点所走路程为
 ×2=
×2=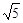 ,到达DE中点.正方形 PQEN运动到图形位置,EQ=1,GP=
,到达DE中点.正方形 PQEN运动到图形位置,EQ=1,GP=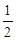 NP为NP中点.
NP为NP中点.
当4≤t≤5时,DP=t-3 设NP与DF相交与点R则PR=
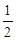 (t-3) 由勾股定理得DR=
(t-3) 由勾股定理得DR= (t-3) 此时DG=
(t-3) 此时DG= t-
t- =
= (t-3) 所以点R与点G重合.
(t-3) 所以点R与点G重合.

练习册系列答案
相关题目
 与
与 交于点A(1,3),过点A作x轴的平行线,分别交两条抛物线于点B,C.下列结论:①
交于点A(1,3),过点A作x轴的平行线,分别交两条抛物线于点B,C.下列结论:①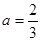 ;②
;②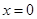 时,
时, ;③平行于x轴的直线
;③平行于x轴的直线 与两条抛物线有四个交点;④2AB=3AC.其中错误结论的个数是( )
与两条抛物线有四个交点;④2AB=3AC.其中错误结论的个数是( )
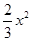 的图象如图,点A0位于坐标原点,点A1,A2,A3…An在y轴的正半轴上,点B1,B2,B3…Bn在二次函数位于第一象限的图象上,点C1,C2,C3…Cn在二次函数位于第二象限的图象上,四边形A0B1A1C1,四边形A1B2A2C2,四边形A2B3A3C3…四边形An﹣1BnAnCn都是菱形,∠A0B1A1=∠A1B2A1=∠A2B3A3…=∠An1BnAn
的图象如图,点A0位于坐标原点,点A1,A2,A3…An在y轴的正半轴上,点B1,B2,B3…Bn在二次函数位于第一象限的图象上,点C1,C2,C3…Cn在二次函数位于第二象限的图象上,四边形A0B1A1C1,四边形A1B2A2C2,四边形A2B3A3C3…四边形An﹣1BnAnCn都是菱形,∠A0B1A1=∠A1B2A1=∠A2B3A3…=∠An1BnAn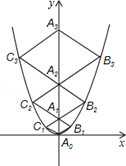



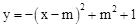 有最大值4,则实数m的值为( )
有最大值4,则实数m的值为( )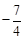 (B)
(B)  或
或 (c)2或
(c)2或 的最小值为负数,则m的取值范围是( )
的最小值为负数,则m的取值范围是( ) 化为
化为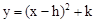 的形式,结果为( )
的形式,结果为( )