题目内容
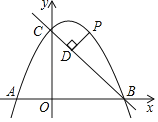
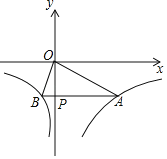
【题目】如图,在平面直角坐标系中,抛物线y=ax2+bx+c(a≠0)与x轴交于点A(-2,0),B(4,0),与直线![]() 交于点C(0,-3),直线
交于点C(0,-3),直线![]() 与x轴交于点D.
与x轴交于点D.
(1)求该抛物线的解析式.
(2)点P是抛物线上第四象限上的一个动点,连接PC,PD,当△PCD的面积最大时,求点P的坐标.
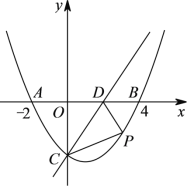
【答案】(1)y=![]() x2
x2![]() x-3;(2)P点坐标为(3,
x-3;(2)P点坐标为(3,![]() ).
).
【解析】
(1)根据C(0,-3),可得c=-3,将A、B坐标代入y=ax2+bx-3得即可求解.
(2)连接OP,设P(m,![]() ),其中:0<m<4,由S△PCD=S△ODP+S△OCP-S△OCD即可求解.
),其中:0<m<4,由S△PCD=S△ODP+S△OCP-S△OCD即可求解.
(1)∵C(0,-3),
∴c=-3,
将A、B坐标代入y=ax2+bx-3得:
![]() ,
,
解得: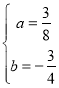 ,
,
∴抛物线的解析式为:y=![]() x2
x2![]() x-3.
x-3.
(2)![]() 中,当y=0时,x=2,即D(2,0),
中,当y=0时,x=2,即D(2,0),
连接OP,
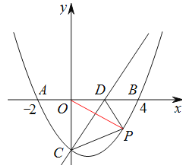
设P(m,![]() m2
m2![]() m-3),其中:0<m<4,
m-3),其中:0<m<4,
S△PCD=S△ODP+S△OCP-S△OCD
=![]()
=![]() ,
,
∵![]() <0,
<0,
∴当m=3时,△PCD的面积取最大值,最大值为![]() ,此时P点坐标为(3,
,此时P点坐标为(3,![]() ).
).

练习册系列答案
相关题目
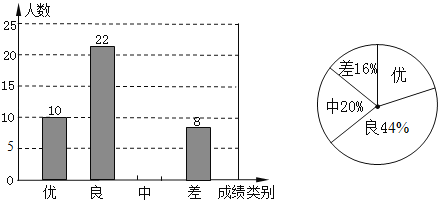
【题目】今年5月份,十八中九年级学生参加了中考体育模拟考试,为了了解该校九年级(1)班同学的中考体育情况,对全班学生的中考体育成绩进行了统计,并绘制以下不完整的频数分布表和扇形统计图,根据图表中的信息解答下列问题:
分组 | 分数段(分)) | 频数 |
A | 26≤x<31 | 2 |
B | 31≤x<36 | 5 |
C | 36≤x<41 | 15 |
D | 41≤x<46 | m |
E | 46≤x<51 | 10 |
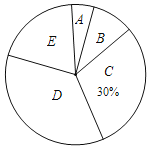
(1)求全班学生人数和m的值.
(2)求扇形统计图中的E对应的扇形圆心角的度数;
(3)该班中考体育成绩满分共有3人,其中男生2人,女生1人,现需从这3人中随机选取2人到八年级进行经验交流,请用“列表法”或“画树状图法”求出恰好选到一男一女的概率.