题目内容
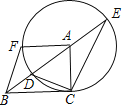
【题目】如图,![]() 中,
中,![]() 是
是![]() 边上一点,
边上一点,![]() ,
,![]() ,
,![]() ,点
,点![]() ,
,![]() 分别是
分别是![]() ,
,![]() 边上的动点,且始终保持
边上的动点,且始终保持![]() .
.


(1)求![]() 的长;
的长;
(2)若四边形![]() 为平行四边形时,求
为平行四边形时,求![]() 的周长;
的周长;
(3)将![]() 沿它的一条边翻折,当翻折前后两个三角形组成的四边形为菱形时,求线段
沿它的一条边翻折,当翻折前后两个三角形组成的四边形为菱形时,求线段![]() 的长.
的长.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)BP=
;(3)BP=![]() 或3或
或3或![]() .
.
【解析】
(1)先根据题意推出△ABE是等腰直角三角形,再根据勾股定理计算即可.
(2)首先要推出△CPQ是等腰直角三角形,再根据已知推出各边的长度,然后相加即可.
(3)首先证明△BPE∽△CQP,然后分三种情况讨论,分别求解,即可解决问题.
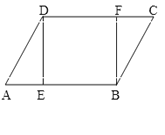
(1)∵四边形ABCD是平行四边形,
∴AB=CD,
∵BE=CD=3,
∴AB=BE=3,
又∵∠A=45°,
∴∠BEA=∠A=45°,∠ABE=90°,
根据勾股定理得AE=![]() =
=![]() ;
;
(2)∵四边形ABCD是平行四边形,
∴AB=CD,∠A=∠C=45°,
又∵四边形ABPE是平行四边形,
∴BP∥AB,且AE=BP,
∴BP∥CD,
∴ED=CP=![]() ,
,
∵∠EPQ=45°,
∴∠PQC=∠EPQ=45°,
∴∠PQC=∠C=45°,∠QPC=90°,
∴CP=PQ=![]() ,QC=2,
,QC=2,
∴△CPQ的周长=2![]() +2;
+2;
(3)解:如图,作BH⊥AE于H,连接BE.

∵四边形ABCD是平行四边形,
∴AB=CD=3,AD=BC=AE+ED=![]() ,∠A=∠C=45°,
,∠A=∠C=45°,
∴AH=BH=![]() ,HE=AD-AH-DE=
,HE=AD-AH-DE=![]()
∴BH=EH,
∴∠EBH=∠HEB=∠EBC=45°,
∴∠EBP=∠C=45°,
∵∠BPQ=∠EPB+∠EPQ=∠C+∠PQC,∠EPQ=∠C,
∴∠EPB=∠PQC,
∴△BPE∽△CQP.
①当QP=QC时,则BP=PE,
∴∠EBP=∠BEP=45°,则∠BPE=90°,
∴四边形BPEF是矩形,
BP=EF=![]() ,
,
②当CP=CQ时,则BP=BE=3,
③当CP=PQ时,则BE=PE=3,∠BEP=90°,
∴△BPE为等腰三角形,
∴BP2=BE2+PE2,
∴BP=![]() ,
,
综上:BP=![]() 或3或
或3或![]() .
.

 阅读快车系列答案
阅读快车系列答案