题目内容
 13、
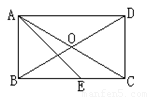
13、 (Ⅰ)已知:如图,平行四边形ABCD的对角线AC、BD相交于点O,EF过点O与AB、CD分别相交于点E、F.
(Ⅰ)已知:如图,平行四边形ABCD的对角线AC、BD相交于点O,EF过点O与AB、CD分别相交于点E、F.求证:BE=DF.
(Ⅱ)请写出使如图所示的四边形ABCD为平行四边形的条件(例如,填:AB∥CD且AD∥BC.在不添加辅助线的情况下,写出除上述条件外的另外四组条件,将答案直接写在下面的横线上.)
(1):
∠DAB=∠DCB且∠ADC=∠ABC
;(2):
AB=CD且AD=BC
;(3):
OA=OC且OD=OB
;(4):
AB∥CD且∠DAB=∠DCB
.分析:(1)运用平行四边形的性质得到相关的线段、角相等即可;
(2)熟悉平行四边形的判定方法.
(2)熟悉平行四边形的判定方法.
解答:证明:(Ⅰ)在平行四边形ABCD中,
 ∵AB∥CD,
∵AB∥CD,
∴∠1=∠2,∠3=∠4.
又∵OB=OD,
∴△BEO≌△DFO,
∴BE=DF.
(Ⅱ)(1)∠DAB=∠DCB且∠ADC=∠ABC(或两组对角分别相等);
(2)AB=CD且AD=BC(或两组对边分别相等);
(3)OA=OC且OD=OB(或O是AC和BD的中点;或AC与BD互相平分;或对角线互相平分);
(4)AD∥BC且AD=BC(或AB∥DC且AB=DC;或一组对边平行且相等);AB∥CD且∠DAB=∠DCB(或一组对边平行且一组对角相等).
 ∵AB∥CD,
∵AB∥CD,∴∠1=∠2,∠3=∠4.
又∵OB=OD,
∴△BEO≌△DFO,
∴BE=DF.
(Ⅱ)(1)∠DAB=∠DCB且∠ADC=∠ABC(或两组对角分别相等);
(2)AB=CD且AD=BC(或两组对边分别相等);
(3)OA=OC且OD=OB(或O是AC和BD的中点;或AC与BD互相平分;或对角线互相平分);
(4)AD∥BC且AD=BC(或AB∥DC且AB=DC;或一组对边平行且相等);AB∥CD且∠DAB=∠DCB(或一组对边平行且一组对角相等).
点评:本题考查了平行四边形的判定与性质,熟练掌握性质定理和判定定理是解题的关键.平行四边形的五种判定方法与平行四边形的性质相呼应,每种方法都对应着一种性质,在应用时应注意它们的区别与联系.

练习册系列答案
相关题目
 (2013•金华模拟)已知:如图,在坡度为i=1:2.4的斜坡BQ上有一棵香樟树PQ,柳明在A处测得树顶点P的仰角为α,并且测得水平的AB=8米,另外BQ=13米,tanα=0.75.点A、B、P、Q在同一平面上,PQ⊥AB.求:香樟树PQ的高度.
(2013•金华模拟)已知:如图,在坡度为i=1:2.4的斜坡BQ上有一棵香樟树PQ,柳明在A处测得树顶点P的仰角为α,并且测得水平的AB=8米,另外BQ=13米,tanα=0.75.点A、B、P、Q在同一平面上,PQ⊥AB.求:香樟树PQ的高度.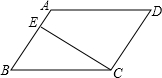 (2013•平南县二模)已知:如图:在?ABCD中,CE⊥AB,E为垂足,如果∠A=125°,则∠BCE的度数是( )
(2013•平南县二模)已知:如图:在?ABCD中,CE⊥AB,E为垂足,如果∠A=125°,则∠BCE的度数是( ) 已知:如图,一架直升飞机在距地面450米上空的P点,测得A地的俯角为30°,B地的俯角为60°(点P和AB所在的直线在同一垂直平面上),求A、B两地间的距离.
已知:如图,一架直升飞机在距地面450米上空的P点,测得A地的俯角为30°,B地的俯角为60°(点P和AB所在的直线在同一垂直平面上),求A、B两地间的距离.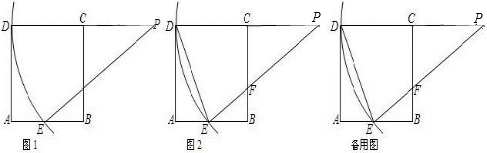
 的两条对角线相交于点
的两条对角线相交于点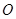 ,
,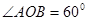 ,
,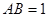 ,
,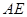 平分
平分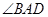 交
交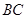 于点
于点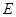 .则
.则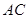 的长为
,
的长为
,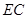 的长为
.
的长为
.