题目内容
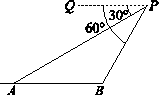
 已知:如图,一架直升飞机在距地面450米上空的P点,测得A地的俯角为30°,B地的俯角为60°(点P和AB所在的直线在同一垂直平面上),求A、B两地间的距离.
已知:如图,一架直升飞机在距地面450米上空的P点,测得A地的俯角为30°,B地的俯角为60°(点P和AB所在的直线在同一垂直平面上),求A、B两地间的距离.分析:过P作AB的垂线,垂足是C,根据两个俯角的度数可知△ABP是等腰三角形,AB=BP,在直角△PBC中,根据三角函数就可求得BP的长.
解答:解: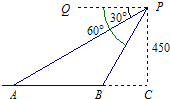 过P作AB的垂线,垂足是C,
过P作AB的垂线,垂足是C,
∵∠A=30°,∠PBC=60°,
∴∠APB=60°-30°,
∴∠APB=∠A,
∴AB=PB.
在Rt△BCP中,∠C=90°,∠PBC=60°,PC=450米,
所以PB=
=
=300
.
所以AB=PB=300
,
答:A、B两地间的距离为:300
米.
 过P作AB的垂线,垂足是C,
过P作AB的垂线,垂足是C,∵∠A=30°,∠PBC=60°,
∴∠APB=60°-30°,
∴∠APB=∠A,
∴AB=PB.
在Rt△BCP中,∠C=90°,∠PBC=60°,PC=450米,
所以PB=
| 450 |
| sin60° |
| 900 | ||
|
| 3 |
所以AB=PB=300
| 3 |
答:A、B两地间的距离为:300
| 3 |
点评:本题主要考查了俯角的定义,正确理解解直角三角形的条件,熟练运用三角函数是解题关键.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案
相关题目
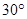 ,B地的俯角为
,B地的俯角为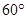 (点P和AB所在 的直线在同一垂直平面上),求A、B两地间的距离.
(点P和AB所在 的直线在同一垂直平面上),求A、B两地间的距离.

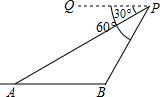 已知:如图,一架直升飞机在距地面450米上空的P点,测得A地的俯角为30°,B地的俯角为60°(点P和AB所在的直线在同一垂直平面上),求A、B两地间的距离.
已知:如图,一架直升飞机在距地面450米上空的P点,测得A地的俯角为30°,B地的俯角为60°(点P和AB所在的直线在同一垂直平面上),求A、B两地间的距离.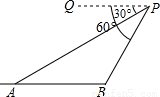
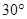 ,B地的俯角为
,B地的俯角为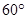 (点P和AB所在 的直线在同一垂直平面上),求A、B两地间的距离.
(点P和AB所在 的直线在同一垂直平面上),求A、B两地间的距离.