题目内容
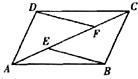24、已知：如图，E，F是平行四边形ABCD的对角线AC上的两点，AE=CF．求证：（1）△CBE≌△ADF；
（2）试判断EB与DF的位置关系，并说明理由．
分析：根据平行四边形的性质，对边相等，对角相等，对角线平分对角，然后根据已知条件转化求证．
解答：证明：（1）∵E，F是平行四边形ABCD的对角线AC上的两点，
∴∠BCE=∠DAF，
∵AE=CF，
∴EC=CF+EF，AF=AE+EF．
∴AF=EC．
又∵四边形ABCD是平行四边形，
∴AD=BC．
∴△CBE与△ADF满足边角边相等的条件．
∴△CBE≌△ADF．
（2）∵△CBE≌△ADF，
∴∠DFE=∠FEB．
∴EB∥DF．
∴∠BCE=∠DAF，
∵AE=CF，
∴EC=CF+EF，AF=AE+EF．
∴AF=EC．
又∵四边形ABCD是平行四边形，
∴AD=BC．
∴△CBE与△ADF满足边角边相等的条件．
∴△CBE≌△ADF．
（2）∵△CBE≌△ADF，
∴∠DFE=∠FEB．
∴EB∥DF．
点评：本题利用平行四边形的性质求证角的相等关系，确定边的相等关系，从而得到判定全等三角形的条件．
练习册系列答案
相关题目
交⊙O于F，GF切⊙O于F且与CP交于G，CH切⊙O于C且与AB的延长线交于H，如果GP2=GD•GC，AD平分∠BAP并交HP于M．
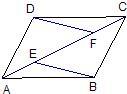24、已知：如图，E、F是四边形ABCD的对角线AC上的两点，AF=CE，DF=BE，DF∥BE．
已知：如图正方形ABCD，E是BC的中点，F在AB上，且BF=
已知：如图，A、C是?DEBF的对角线EF所在直线上的两点，且AE=CF．