题目内容
已知：如图，B、C是线段AD上两点，且AB：BC：CD=2：4：3，M是AD的中点，CD=6cm，求线段MC的长．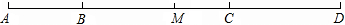
分析：首先由已知AB：BC：CD=2：4：3，CD=6cm，求出AD，再由M是AD的中点，求出DM，从而求出MC的长．
解答：解：由AB：BC：CD=2：4：3，设AB=2xcm，BC=4xcm，CD=3xcm，…1分
则CD=3x=6，解得x=2． …2分
因此，AD=AB+BC+CD=2x+4x+3x=18（cm）．…4分
因为点M是AD的中点，所以DM=
AD=
×18=9（cm）．…6分
MC=DM-CD=9-6=3（cm）．…7分
则CD=3x=6，解得x=2． …2分
因此，AD=AB+BC+CD=2x+4x+3x=18（cm）．…4分
因为点M是AD的中点，所以DM=
| 1 |
| 2 |
| 1 |
| 2 |
MC=DM-CD=9-6=3（cm）．…7分
点评：此题考查的知识点是两点间的距离，关键是先由已知求出AD的长，再求MC的长．
练习册系列答案
相关题目
交⊙O于F，GF切⊙O于F且与CP交于G，CH切⊙O于C且与AB的延长线交于H，如果GP2=GD•GC，AD平分∠BAP并交HP于M．
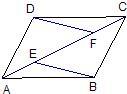24、已知：如图，E、F是四边形ABCD的对角线AC上的两点，AF=CE，DF=BE，DF∥BE．
已知：如图正方形ABCD，E是BC的中点，F在AB上，且BF=
已知：如图，A、C是?DEBF的对角线EF所在直线上的两点，且AE=CF．