��Ŀ����
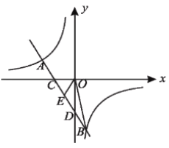
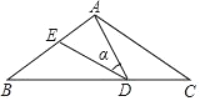
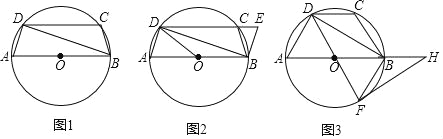
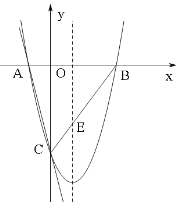
����Ŀ����ͼ��һ�κ���y =��4x��4��ͼ����x�ᡢy��ֱ���A��C���㣬������y=![]() ��ͼ��A��C���㣬����x�ύ�ڵ�B��
��ͼ��A��C���㣬����x�ύ�ڵ�B��
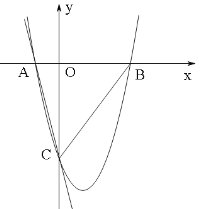
��1���������ߵĺ�������ʽ��
��2���������ߵĶԳ�������һ��E,ʹ��E����A�ľ����뵽��C�ľ���֮����С������˵�E�����ꣻ
��3����ֱ��MNƽ����x�ᣬ�ֱ��߶�AC��BC�ڵ�M��N������x�����Ƿ���ڵ�P��ʹ�á�PMN�ǵ���ֱ�������Σ�������ڣ������������������P������ꣻ��������ڣ���˵�����ɣ�
���𰸡���1��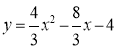 ����2��E
����2��E![]() ����3��
����3��![]() ��
��![]() ��
��![]()
��������
��1�����һ�κ���y =��4x��4�������ύ��A��C�����꣬���������߽���ʽ������⼴�ɣ�
��2����A����B���������߶Գ���x=1�Գƣ���B��E��C���㹲��ʱ����E����A�ľ����뵽��C�ľ���֮����С����y=0�����B�����꣬�ô���ϵ�������BC����ʽ��BC��Գ���Ľ��㼴ΪE�㣻
��3����ֱ�Ƕ�����з��࣬��3���������M��N��������Ϊa����ʾ����Ӧ�߶Σ��ٸ��ݵ���ֱ�������ε����ʽ�����⼴�ɣ�
�⣺��1����һ�κ���y=��4x��4��ͼ����x�ᡢy��ֱ���A��C���㣬
��A ����1��0����C ��0����4����
��A ����1��0����C ��0����4������![]() ��
��
��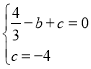 �����
����� ����
����
��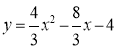 ��
��
��2����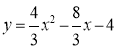 =
=![]() ��
��
�Գ�����ֱ��x=1��
��A, B����ֱ��x=1�Գ�
��ֱ��BC��Գ���ֱ��x=1�Ľ��㼴ΪE��
��ʱ��E����A�ľ����뵽��C�ľ���֮����С��
��y=0����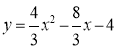 ����
����![]() ��
��
�����![]() ��
��![]() ��
��
��B![]() ����C
����C![]() ��
��
����ֱ��CB�Ľ���ʽΪ![]() ��
��
��x=1����![]() ����y=
����y=![]() ��
��
��E![]() ��
��
��3����DP��AB
��M��N��������Ϊa��
AC����ֱ�ߵĽ���ʽΪy=��4x��4, BC����ֱ�ߵĽ���ʽΪ��![]() ��
��
��M![]() ��N
��N![]() ��
��
�ٵ���PMN=90����MN=a+4��PM=��a����Ϊ�ǵ���ֱ�������Σ���a=a+4 ��a=��2 ��P�ĺ�����Ϊ![]() ��
��
��P������Ϊ![]() ��
��
�ڵ���PNM=90����PN=MN��ͬ�ϣ�a=��2����P�ĺ�����Ϊ![]() ��
��
��P������Ϊ![]() ��
��
�۵���MPN=90������MN���е�Q������PQ����PQ=��a��
��PM=PN����PQ��MN����MN=2PQ������a+4=��2a��
��ã�a=![]() ��
��
��P�ĺ�����Ϊ��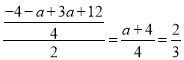 ����
����
��P�������Ϊ![]() ��
��
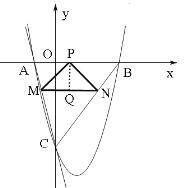
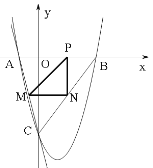
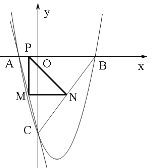
�ۺ�����P����Ϊ![]() ��
��![]() ��
��![]() ��
��