题目内容
【题目】如图,在△ABC中,AB=AC,点M在BA的延长线上.

(1)按下列要求作图,并在图中标明相应的字母(尺规作图,保留作图痕迹,不要求写作法和证明);
①作∠MAC的平分线AN;
②在AN上截取AD=BC,连结CD.
(2)在(1)的条件下,判断四边形ABCD的形状,并证明你的结论.
【答案】(1)①详见解析;②详见解析;(2)四边形ABCD是平行四边形,详见解析
【解析】
(1)作一个角的平分线,和线段的定义即可完成作图;
(2)由等腰三角形的性质和角平分线的性质,得到∠MAD =∠ABC,则AD∥BC,即可得到结论成立.
解:(1)如图所示为所求的图形;
(2)四边形ABCD是平行四边形.理由如下:
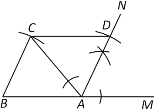
∵AB=AC,
∴∠ABC=∠ACB,
∵AN平分∠MAC,
∴∠CAD=∠MAD,
∵∠CAD+∠MAD=∠ABC+∠ACB,
∴∠MAD =∠ABC,
∴AD∥BC,
∵AD=BC,
∴四边形ABCD是平行四边形.

练习册系列答案
相关题目