题目内容
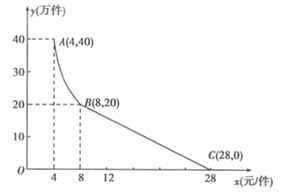
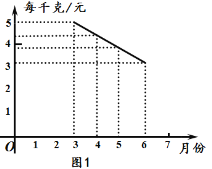
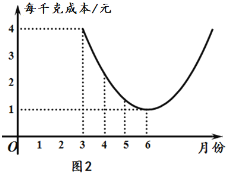
【题目】某种蔬菜的销售单价y1与销售月份x之间的关系如图1所示,成本y2与销售月份x之间的关系如图2所示.
(1)已知6月份这种蔬菜的成本最低,此时出售每干克的收益是多少元?(收益=售价-成本)
(2)分别求出y1、y2与x之间的函数关系式;
(3)哪个月出售这种蔬菜,每千克的收益最大?说明理由.
【答案】(1)6月份出售这种蔬菜每千克的收益是2元.(2)y1=﹣![]() +7;y2=
+7;y2=![]() x2﹣4x+13.(3)5月份出售这种蔬菜,每千克的收益最大.
x2﹣4x+13.(3)5月份出售这种蔬菜,每千克的收益最大.
【解析】
(1)根据收益=售价-成本,由图像,得到当x=6时,y1=3,y2=1.所以,收益为2元.(2)根据图像设![]() ,
, ![]() .再代入点坐标进行作答.(3)由收益=售价-成本,得到收益= y1﹣y2,即﹣
.再代入点坐标进行作答.(3)由收益=售价-成本,得到收益= y1﹣y2,即﹣![]() x+7﹣(
x+7﹣(![]() x2﹣4x+13).化简,得到5月份出售这种蔬菜,每千克的收益最大.
x2﹣4x+13).化简,得到5月份出售这种蔬菜,每千克的收益最大.
解:(1)当x=6时,y1=3,y2=1,
∵y1﹣y2=3﹣1=2,
∴6月份出售这种蔬菜每千克的收益是2元.
(2)设![]() ,
, ![]() .
.
将(3,5)、(6,3)代入![]() ,
,
解得:
∴y1=﹣![]() +7;
+7;
将(3,4)代入y2=a(x﹣6)2+1,
4=a(3﹣6)2+1,解得:a=![]() ,
,
∴y2=![]() (x﹣6)2+1
(x﹣6)2+1
=![]() x2﹣4x+13.
x2﹣4x+13.
(3)5月份出售这种蔬菜,每千克的收益最大,理由:
∵y1﹣y2=﹣![]() x+7﹣(
x+7﹣(![]() x2﹣4x+13)
x2﹣4x+13)
=﹣![]() x2+
x2+![]()
![]() x﹣6
x﹣6
=﹣![]()
![]()
∴当x=5时,y1﹣y2取最大值,最大值为![]() ,
,
即5月份出售这种蔬菜,每千克的收益最大.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目