题目内容
【题目】如图,在△ABC中,AB=AC=10,点D是BC边上的一动点(不与B、C重合),∠ADE=∠B=∠α,DE交AB于点E,且tan∠α=0.75,有以下的结论:
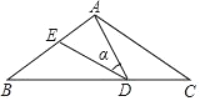
①△DBE∽△ACD;②△ADE∽△ACD;③△BDE为直角三角形时,BD为8或3.5;
④0<BE≤5.其中正确的结论是_______(填入正确结论的序号)
【答案】①③
【解析】①∵AB=AC,∴∠B=∠C,又∵∠ADE=∠B∴∠ADC=180°﹣α﹣∠BDE,
∵∠BED=180°﹣α﹣∠BDE,∴∠BED=∠ADC∴△DBE∽△ACD,故①正确;
②∵∠B=∠C,∴∠C=∠ADE,不能得到△ADE∽△ACD;故②错误,
③当∠AED=90°时,由①可知:△ADE∽△ABD,∴∠ADB=∠AED,
∵∠AED=90°,∴∠ADB=90°,即AD⊥BC,
∵AB=AC,∴BD=CD,∴∠ADE=∠B=α且cosα=0.8,AB=10,BD=8.
当∠BDE=90°时,易△BDE∽△CAD,∵∠BDE=90°,∴∠CAD=90°,
∵∠B=α且cosα=0.8.AB=10,∴cosC=0.8,∴CD=12.5,∴BD=BC﹣CD=3.5;故③正确.
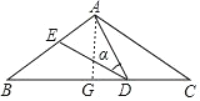
④过A作AG⊥BC于G,∵cosα=0.8,∴BG=8,∴BC=16,易证得△BDE∽△CAD,
设BD=y,BE=x,∴ ![]() ,∴∴
,∴∴ ![]() ,整理得:y2﹣16y+64=64﹣10x,
,整理得:y2﹣16y+64=64﹣10x,
即(y﹣8)2=64﹣10x,∴0<x≤6.4.故④错误.故答案为:①③.

练习册系列答案
相关题目