题目内容
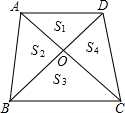如图所示，已知AC⊥BD于点O，△AOD、△AOB、△BOC、△COD的面积分别为S1、S2、S3、S4，设AC=m，BD=n，则下式中正确的是（ ）A、S1+S2+S3+S4=
| ||
| B、S1+S2+S3+S4=mn | ||
C、S1•S2•S3•S4=
| ||
| D、S1•S2•S3•S4=mn |
分析：根据三角形的面积公式可得出S1，S2，S3，S4，再代入数值计算即可．
解答：解：∵S1=
，
S2=
，
S3=
，
S4=
，
∴S1+S2+S3+S4=
=
=
，
∵AC=m，BD=n，
∴S1+S2+S3+S4=
mn．
故选A．
| AO•DO |
| 2 |
S2=
| AO•BO |
| 2 |
S3=
| BO•CO |
| 2 |
S4=
| CO•DO |
| 2 |
∴S1+S2+S3+S4=
| AO•DO+AO•BO+BO•CO+CODO |
| 2 |
=
| A0(BO+DO)+CO(BO+DO) |
| 2 |
=
| AC•BD |
| 2 |
∵AC=m，BD=n，
∴S1+S2+S3+S4=
| 1 |
| 2 |
故选A．
点评：本题考查了三角形面积的计算，熟记三角形的面积公式是解题的关键．
练习册系列答案
名校课堂系列答案
相关题目
某厂房屋顶呈人字架形（等腰三角形），如图所示，已知AC=BC=8m，∠A=30°，CD⊥AB于点D．
28、如图所示，已知AC⊥BD于点P，AP=CP，请添加一个条件，使BP=DP，并给予证明．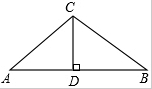
某厂房屋顶呈人字架形（等腰三角形），如图所示，已知AC=BC=10m，∠A=30°，CD⊥AB于点D，则AB=
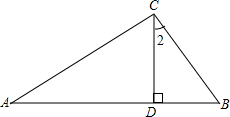如图所示，已知AC⊥BC，CD⊥AB，∠2与∠A有什么关系？请说明理由．