题目内容
 某厂房屋顶呈人字架形(等腰三角形),如图所示,已知AC=BC=10m,∠A=30°,CD⊥AB于点D,则AB=
某厂房屋顶呈人字架形(等腰三角形),如图所示,已知AC=BC=10m,∠A=30°,CD⊥AB于点D,则AB=10
m
| 3 |
10
m
(结果保留根号).| 3 |
分析:据等腰三角形的性质,可求得∠B的度数,从而在RT△ACD和RT△BCD中,分别利用三角函数的知识可求出AD、BD,从而可得出AB的长度.
解答:解:∵AC=BC=10m,∠A=30°,
∴∠B=∠A=30°,
在RT△ACD中,AD=ACcos∠A=5
m
在RT△BCD中,BD=BCcos∠B=5
m,
故可得AB=AD+BD=10
m.
故答案为:10
m.
∴∠B=∠A=30°,
在RT△ACD中,AD=ACcos∠A=5
| 3 |
在RT△BCD中,BD=BCcos∠B=5
| 3 |
故可得AB=AD+BD=10
| 3 |
故答案为:10
| 3 |
点评:此题考查了勾股定理的应用及等腰三角形的性质,解答本题的关键是利用三角函数的知识分别求出AD及BD的长度.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 某厂房屋顶呈人字架形(等腰三角形),如图所示,已知AC=BC=8m,∠A=30°,CD⊥AB于点D.
某厂房屋顶呈人字架形(等腰三角形),如图所示,已知AC=BC=8m,∠A=30°,CD⊥AB于点D. 某厂房屋顶呈人字架形(等腰三角形),如图所示,已知AC=BC=10m,∠A=30°,CD⊥AB于点D,求AB的长.(结果保留根号)
某厂房屋顶呈人字架形(等腰三角形),如图所示,已知AC=BC=10m,∠A=30°,CD⊥AB于点D,求AB的长.(结果保留根号) m,
m, ,
,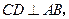 于点
于点

 的大小.
的大小. 的长度.
的长度. m,
m, ,
, 于点
于点

 的大小.
的大小. 的长度.
的长度.