Question

【题目】如图，矩形ABCD中，AB=6，AD=8，点E在边AD上，且AE：ED=1：3．动点P从点A出发，沿AB 运动到点B停止．过点E作EF⊥PE交射线BC于点F，设M是线段EF的中点，则在点P运动的整个过程中，点M运动路线的长为______．

Answer 1

【答案】4

【解析】过点M作GH⊥AD，证明△EGM≌△FHM，得到MG=MH，从而可知：点M的轨迹是一条平行于BC的线段，然后证明△EF1B∽△∠EF1F2，求得F1F2=8，最后根据三角形中位线定理可求得答案．

解：如图所示：过点M作GH⊥AD.

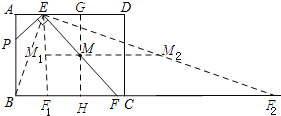
∵AD∥CB，GH⊥AD，

∴GH⊥BC.

在△EGM和△FHM中，

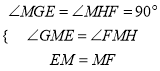
∴△EGM≌△FHM.

∴MG=MH.

∴点M的轨迹是一条平行于BC的线段

当点P与A重合时,BF1=AE=2，

当点P与点B重合时,∠F2+∠EBF1=90,∠BEF1+∠EBF1=90，

∴∠F2=∠EBF1.

∵∠EF1B=∠EF1F2，

∴△EF1B∽△∠EF1F2.

∴，

即

∴F1F2=8，

∵M1M2是△EF1F2的中位线，

∴M1M2= F1F2=4.

故答案为：4.