Question

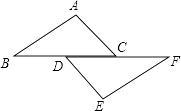
【题目】如图①，在△ABC中，D、E分别是AB，AC上的点，AB=AC，AD=AE，然后将△ADE绕点A顺时针旋转一定角度，连接BD，CE，得到图②，将BD，CE分别延长至M，N，使DM= BD，EN= CE，连接AM，AN，MN得到图③，请解答下列问题：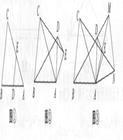

（1）在图②中，BD与CE的数量关系是；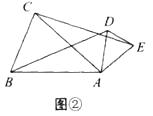

（2）在图③中，猜想AM与AN的数量关系，∠MAN与∠BAC的数量关系，并证明你的猜想.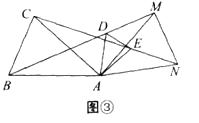

Answer 1

【答案】
（1）BD=CE
（2）解：AM=AN，∠MAN=∠BAC

∵ ∠DAE=∠BAC

∴ ∠CAE=∠BAD

在△BAD和△CAE中，

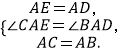
∴ △CAE≌△BAD（SAS）

∴ ∠ACE=∠ABD ，CE=BD

∵ DM= BD，EN= CE，BD=CE，

∴ BM=CN

在△ABM和△ACN中，

∴ △ABM≌△ACN（SAS）

∴ AM=AN， ∠BAM=∠CAN，∴∠MAN=∠BAC.

【解析】（1）BD=CE，理由如下：由旋转的性质可知BAD=CAE，又因AB=AC,AD=AE,由SAS判断出△BAD△CAE,根据全等三角形对应边相等得出结论；
（2）首先由SAS判断出△CAE≌△BAD，由全等三角形的性质得出 ∠ACE=∠ABD，CE=BD，从而得出 BM=CN，然后由SAS判断出 △ABM≌△ACN，根据全等三角形的性质得出 AM=AN， ∠BAM=∠CAN，从而得出即∠MAN=∠BAC.