题目内容
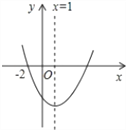
【题目】如图,二次函数y=ax2+bx+c(a≠0)的图象过(﹣2,0),则下列结论:①bc>0;②b+2a=0;③a+c>b;④16a+4b+c=0;⑤3a+c<0.其中正确结论的个数是( )
A. 5 B. 4 C. 3 D. 2
【答案】B
【解析】∵抛物线开口向上,
∴a>0,
∵抛物线的对称轴为直线x=![]() =1,
=1,
∴b=2a<0,
而抛物线与x轴的交点在x轴下方,
∴c<0,
∴bc>0,所以①正确;
∵b=2a,
∴b+2a=0,所以②正确;
∵x=1时,y<0,
∴ab+c<0,即a+c<b,所以③错误;
∵二次函数y=ax+bx+c(a≠0)的图象过(2,0),且对称轴为直线x=1,
∴二次函数y=ax+bx+c(a≠0)的图象过(4,0),
即x=4时,y=0,
∴16a+4b+c=0,所以④正确;
∵ab+c<0,b=2a,
∴a+2a+c<0,即3a+c<0,所以⑤正确。
故选B.
点睛:本题考查了二次函数图象与二次函数系数之间的关系,二次函数与方程之间的转换,跟的判别式的熟练运用,会利用特殊值代入法求得特殊的式子,然后根据图象判断其值.

练习册系列答案
相关题目
【题目】小强与小刚两位同学在学习“概率”时,做抛骰子(均匀立方体形状)试验,他们共抛了54次,出现不同向上点数的次数如下表:
向上点数 | 1 | 2 | 3 | 4 | 5 | 6 |
出现次数 | 6 | 9 | 5 | 8 | 16 | 10 |
(1)请计算出现向上点数为3的频率及出现向上点数为5的频率.
(2)小强说:“根据试验,一次试验中出现向上点数为5的概率最大.”小刚说:“如果抛540次,那么出现向上点数为6的次数正好是100次.”请判断小强和小刚说法的对错.
(3)如果小强与小刚各抛一枚骰子,求出现向上点数之和为3的倍数的概率.
