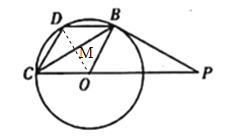
[题目]如图所示.PB是⊙O的切线.B为切点.圆心O在PC上.∠P=30°.D为弧BC的中点.(1)求证:PB=BC,(2)试判断四边形BOCD的形状.并说明理由. 题目和参考答案——青夏教育精英家教网—

题目内容

【题目】如图所示，PB是⊙O的切线，B为切点，圆心O在PC上，∠P=30°，D为弧BC的中点.

(1)求证：PB=BC；

(2)试判断四边形BOCD的形状，并说明理由.

【答案】（1）见解析；（2）菱形

【解析】

试题（1）由切线的性质得到∠OBP=90°，进而得到∠BOP=60°，由OC=BO，得到∠OBC=∠OCB=30°，由等角对等边即可得到结论；

（2）由对角线互相垂直平分的四边形是菱形证明即可．

试题解析：证明：（1）∵PB是⊙O的切线，∴∠OBP=90°，∠POB=90°-30°=60°．∵OB=OC，∴∠OBC=∠OCB．∵∠POB=∠OBC+∠OCB，∴∠OCB=30°=∠P，∴PB=BC；

（2）连接OD交BC于点M．∵D是弧BC的中点，∴OD垂直平分BC．

在直角△OMC中，∵∠OCM=30°，∴OC=2OM=OD，∴OM=DM，∴四边形BOCD是菱形．

练习册系列答案

求证：（1）∠BGC=90°+∠BAC；

（2）∠1=∠2．

【题目】如图，在平面直角坐标系中，已知△ABC三个顶点的坐标分别是A（2，2），B（4，0），C（4，﹣4）．

（1）请在图中，画出△ABC向左平移6个单位长度后得到的△A1B1C1；

（2）以点O为位似中心，将△ABC缩小为原来的，得到△A2B2C2，请在图中y轴右侧，画出△A2B2C2，并求出∠A2C2B2的正弦值．

【题目】如图，一次函数y=kx+b与反比例函数y=的图象在第一象限交于点A（4，3），与y轴的负半轴交于点B，且OA=OB．

（1）求一次函数y=kx+b和y=的表达式；

（2）已知点C在x轴上，且△ABC的面积是8，求此时点C的坐标；

（3）反比例函数y=（1≤x≤4）的图象记为曲线C1，将C1向右平移3个单位长度，得曲线C2，则C1平移至C2处所扫过的面积是_________．(直接写出答案)

【题目】已知二次函数y=ax2+bx+c（a≠0）的图象如图所示，有下列5个结论：①abc＜0；②b＜a+c；③4a+2b+c＞0；④2c＜3b；⑤a+b＜m（am+b）（m≠1且为实数），其中正确的个数是（）

A. 2个 B. 3个 C. 4个 D. 5个

【题目】“最美女教师”张丽莉，为抢救两名学生，以致双腿高位截肢，社会各界纷纷为她捐款，我市某中学九年级一班全体同学参加了捐款活动，该班同学捐款情况的部分统计图如图所示：

（1）求该班的总人数；

（2）将条形图补充完整，并写出捐款总额的众数；

（3）该班平均每人捐款多少元？

【题目】铜仁某校高中一年级组建篮球队，对甲、乙两名备选同学进行定位投篮测试，每次投10个球，共投10次.甲、乙两名同学测试情况如图所示：

根据图6提供的信息填写下表：

	平均数	众数	方差
甲
乙

如果你是高一学生会文体委员，会选择哪名同学进入篮球队？请说明理由.

【题目】如图，在△ABC内一点D，点C是AE上一点，AD交BE于点P，射线DC交BE的延长线于点F，且∠ABD＝∠ACD，∠PDB＝∠PDC

(1)求证：AB＝AC；

(2)若AB＝3，AE＝5，求的值；

(3)若，＝m，则＝_______.

【题目】如图，已知点E,F分别是□ABCD的边BC,AD上的中点，且∠BAC=90°．

（1）求证：四边形AECF是菱形；

（2）若∠B=30°，BC=10，求菱形AECF面积．

试题分类