Question

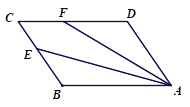
【题目】如图，已知点E,F分别是□ABCD的边BC,AD上的中点，且∠BAC=90°．

（1）求证：四边形AECF是菱形；

（2）若∠B=30°，BC=10，求菱形AECF面积．

Answer 1

【答案】（1）见解析（2）

【解析】

试题（1）利用平行四边形的性质和菱形的性质即可判定四边形AECF是菱形；

（2）连接EF交于点O，运用解直角三角形的知识点，可以求得AC与EF的长，再利用菱形的面积公式即可求得菱形AECF的面积．

试题解析：（1）证明：∵四边形ABCD是平行四边形，

∴AD∥BC，AD=BC．

在Rt△ABC中，∠BAC=90°，点E是BC边的中点，

∴AE=CE=BC．

同理，AF=CF=AD．

∴AF=CE．

∴四边形AECF是平行四边形．

∴平行四边形AECF是菱形．

（2）解：在Rt△ABC中，∠BAC=90°，∠B=30°，BC=10，

∴AC=5，AB=．

连接EF交于点O，

∴AC⊥EF于点O，点O是AC中点．

∴OE=．

∴EF=．

∴菱形AECF的面积是AC·EF=．