题目内容
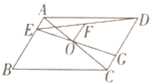
【题目】如图,在凸四边形![]() 中,
中,![]() ,
,![]() .
.
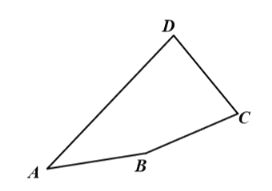
(1)利用尺规,以![]() 为边在四边形内部作等边
为边在四边形内部作等边![]() (保留作图痕迹,不需要写作法).
(保留作图痕迹,不需要写作法).
(2)连接![]() ,判断四边形
,判断四边形![]() 的形状,并说明理由.
的形状,并说明理由.
【答案】(1)见解析;(2)四边形ABCE是菱形,理由见解析.
【解析】
(1)分别以点C、D为圆心,CD长为半径画弧,在四边形ABCD内部交于点E,连接CE、DE即可得;
(2)先证AB∥CE,结合AB=CE可得四边形ABCE是平行四边形,然后由AB=BC可得四边形ABCE是菱形.
解:(1)如图所示,△CDE即为所求:
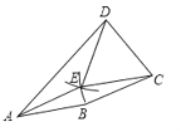
(2)四边形ABCE是菱形,
理由:∵△CDE是等边三角形,
∴∠ECD=60°,CD=DE=CE,
∵∠ABC+∠BCD=240°,
∴∠ABC+∠BCE=180°,
∴AB∥CE,
又∵AB=BC=CD,
∴AB=CE,
∴四边形ABCE是平行四边形,
∵AB=BC,
∴四边形ABCE是菱形.

练习册系列答案
 快乐小博士巩固与提高系列答案
快乐小博士巩固与提高系列答案
相关题目