题目内容
如图,直线AB、CD分别经过点(0,1)和(0,2)且平行于x轴,图1中射线OA为正比例函数y=kx(k>0)在第一象限的部分图象,射线OB与OA关于y轴对称;图2为二次函数y=ax2(a>0)的图象.
(1)如图l,求证:
=
;
(2)如图2,探索:
的值.

(1)如图l,求证:
| AB |
| CD |
| 1 |
| 2 |
(2)如图2,探索:
| AB |
| CD |
分析:(1)根据直线AB经过点(0,1)且平行于x轴,可得yA=1,代入正比例函数y=kx可得A(
,1),根据轴对称的性质可得AB的长,同理可得CD的长,代入计算即可证明
=
;
(2)根据直线AB经过点(0,1)且平行于x轴,可得yA=1,代入二次函数y=ax2(a>0)可得A(
,1),根据轴对称的性质可得AB的长,同理可得CD的长,代入计算即可得到
的值.
| 1 |
| k |
| AB |
| CD |
| 1 |
| 2 |
(2)根据直线AB经过点(0,1)且平行于x轴,可得yA=1,代入二次函数y=ax2(a>0)可得A(
| 1 | ||
|
| AB |
| CD |
解答:(1)证明:由题意得yA=1,
∴A(
,1),
∵B与A关于y轴对称,
∴AB=
.
同理可得:CD=
,
∴
=
;
(2)解:由题意得:A(
,1),B(-
,1),
∴AB=
.
同理可得:CD=
,
∴
=
=
.
∴A(
| 1 |
| k |
∵B与A关于y轴对称,
∴AB=
| 2 |
| k |
同理可得:CD=
| 4 |
| k |
∴
| AB |
| CD |
| 1 |
| 2 |
(2)解:由题意得:A(
| 1 | ||
|
| 1 | ||
|
∴AB=
| 2 | ||
|
同理可得:CD=
2
| ||
|
∴
| AB |
| CD |
| 1 | ||
|
| ||
| 2 |
点评:考查了二次函数综合题,涉及的知识点有:平行于x轴的直线的特点,正比例函数的性质,轴对称的性质,二次函数的性质,解题的关键是得到AB,CD的值.

练习册系列答案
 天天向上口算本系列答案
天天向上口算本系列答案
相关题目
 21、如图,直线AB、CD、EF都经过点O,且AB⊥CD,∠COE=35°,求∠DOF、∠BOF的度数.
21、如图,直线AB、CD、EF都经过点O,且AB⊥CD,∠COE=35°,求∠DOF、∠BOF的度数.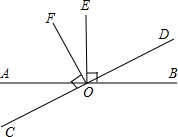 如图,直线AB与CD相交于点O,OE⊥AB,OF⊥CD.
如图,直线AB与CD相交于点O,OE⊥AB,OF⊥CD.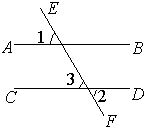 25、完成推理填空:如图:直线AB、CD被EF所截,若已知AB∥CD,
25、完成推理填空:如图:直线AB、CD被EF所截,若已知AB∥CD, 如图,直线AB、CD、EF相交于点O,AB⊥CD,OG平分∠AOE,∠FOD=24°,∠COG的度数=
如图,直线AB、CD、EF相交于点O,AB⊥CD,OG平分∠AOE,∠FOD=24°,∠COG的度数= 如图,直线AB,CD相交于O点,EO⊥CD,垂足为O点,若∠BOE=50°,求∠AOD的度数.
如图,直线AB,CD相交于O点,EO⊥CD,垂足为O点,若∠BOE=50°,求∠AOD的度数.