题目内容
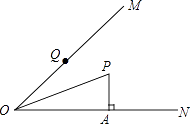
【题目】如图，已知OP平分∠MON，PA⊥ON于点A，点Q是射线OM上的一个动点．若PA=2，则PQ的最小值为 ， 理论根据为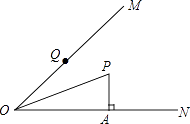 
【答案】2；角平分线上的点到角两边的距离相等
【解析】解：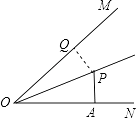 
过P作PQ⊥OM于Q，此时PQ的长最短，
∵OP平分∠MON，PA⊥ON，PA=2，
∴PQ=PA=2（角平分线上的点到角两边的距离相等），
所以答案是：2，角平分线上的点到角两边的距离相等．
【考点精析】通过灵活运用垂线段最短和角平分线的性质定理，掌握连接直线外一点与直线上各点的所有线段中，垂线段最短；现实生活中开沟引水，牵牛喝水都是“垂线段最短”性质的应用；定理1：在角的平分线上的点到这个角的两边的距离相等； 定理2：一个角的两边的距离相等的点，在这个角的平分线上即可以解答此题．
练习册系列答案
相关题目
【题目】某市民政部门举行“即开式福利彩票”销售活动，发行彩票10万张（每张彩票2元），在这些彩票中，设置如下奖项：
奖金（元） | 10000 | 5000 | 1000 | 500 | 100 | 50 |
数量（个） | 1 | 4 | 20 | 40 | 100 | 200 |
如果花2元购买1张彩票，那么所得奖金不少于1000元的概率是
