Question

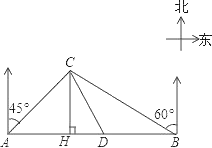
【题目】某大草原上有一条笔直的公路，在紧靠公路相距40千米的A、B两地，分别有甲、乙两个医疗站，如图，在A地北偏东45°，B地北偏西60°方向上有一牧民区C，过点C作CH⊥AB于H．

（1）求牧民区C到B地的距离（结果用根式表示）；

（2）一天，乙医疗队的医生要到牧民区C出诊，她先由B地搭车沿公路AB到D处（BD＜AB）转车，再由D地沿DC方向到牧民区C．若C、D两地距离是B、C两地距离的倍，求B、D两地的距离．（结果精确到0.1千米 参考数据： ≈2.449， ≈1.732， ≈1.414）

Answer 1

【答案】（1）牧民区C到B地的距离为（40﹣40）千米；

（2）BD之间的距离为4.7千米．

【解析】试题分析：（1）设CH为未知数，分别表示出AH，BH的值，让其相加得40求值即可求得CH的长，进而可求得CB的长；

（2）由CD和BC的数量关系可得CD和CH的数量关系，进而可得HD的长，让BH的长减去DH的长即为BD的距离．

试题解析：（1）设CH为x千米，由题意得，∠CBH=30°，∠CAH=45°，

∴AH=CH=x，

在Rt△BCH中，tan30°=，

∴BH=x，

∵AH+HB=AB=40，

∴x+x=40，

解得x=20﹣20，

∴CB=2CH=40﹣40．

答：牧民区C到B地的距离为（40﹣40）千米；

（2）∵C、D 两地距离是B、C两地距离的倍，CH=BC，

∴DC=（40﹣40）=60﹣20，BH=x=（20﹣20）=60﹣20，

∴DH=CH=20﹣20，

∴BD=BH﹣DH=（60﹣20）﹣（20﹣20）=60﹣20﹣20+20≈4.7．

答：BD之间的距离为4.7千米．