题目内容
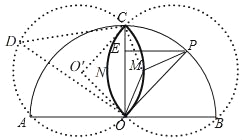
【题目】如图,AB为⊙O的直径,且AB=4,点C在半圆上,OC⊥AB,垂足为点O,P为半圆上任意一点,过P点作PE⊥OC于点E,设△OPE的内心为M,连接OM、PM.当点P在半圆上从点B运动到点A时,内心M所经过的路径长为_____.

【答案】![]()
【解析】
根据三角形内心的性质可求得∠PMO=135°,再由全等三角形的判定和性质可得∠CMO=135°,过C、M、O三点作⊙O′,连O′C,O′O,在优弧CO取点D,连DC,DO,在等腰直接三角形中求得O′O,从而求得弧OMC,同理可求得弧ONC,从而求得点M所经过的路径.
解:∵△OPE的内心为M,
∴∠MOP=∠MOC,∠MPO=∠MPE,
∴∠PMO=180°﹣∠MPO﹣∠MOP=180°﹣![]() (∠EOP+∠OPE),
(∠EOP+∠OPE),
∵PE⊥OC,即∠PEO=90°,
∴∠PMO=180°﹣![]() ×(∠EOP+∠OPE)=180°﹣
×(∠EOP+∠OPE)=180°﹣![]() ×(180°﹣90°)=135°,
×(180°﹣90°)=135°,
如图,连接OC,
∵OP=OC,OM=OM,
而∠MOP=∠MOC,
∴△OPM≌△OCM(SAS),
∴∠CMO=∠PMO=135°,
所以点M在以OC为弦,并且所对的圆周角为135°的两段劣弧上(弧OMC和弧ONC);
点M在扇形BOC内时,
过C、M、O三点作⊙O′,连O′C,O′O,
在优弧CO取点D,连DC,DO,
∵∠CMO=135°,
∴∠CDO=180°﹣135°=45°,
∴∠CO′O=90°,而OA=2cm,
∴O′O=![]() OC=
OC=![]() ×2=
×2=![]() ,
,
∴弧OMC的长=![]() cm,
cm,
同理:点M在扇形AOC内时,同①的方法得,弧ONC的长为![]() cm,
cm,
所以内心M所经过的路径长为2×![]() =
=![]() πcm.
πcm.
故答案为:![]() πcm.
πcm.

 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案【题目】为了弘扬我国古代数学发展的伟大成就,某校九年级进行了一次数学知识竞赛,并设立了以我国古代数学家名字命名的四个奖项:“祖冲之奖”、“刘徽奖”、“赵爽奖”和“杨辉奖”,根据获奖情况绘制成如图1和图2所示的条形统计图和扇形统计图,并得到了获“祖冲之奖”的学生成绩统计表:
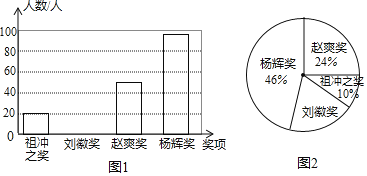
“祖冲之奖”的学生成绩统计表:
分数 | 80 | 85 | 90 | 95 |
人数 | 4 | 2 | 10 | 4 |
根据图表中的信息,解答下列问题:
![]() 这次获得“刘徽奖”的人数是多少,并将条形统计图补充完整;
这次获得“刘徽奖”的人数是多少,并将条形统计图补充完整;
![]() 获得“祖冲之奖”的学生成绩的中位数是多少分,众数是多少分;
获得“祖冲之奖”的学生成绩的中位数是多少分,众数是多少分;
![]() 在这次数学知识竟赛中有这样一道题:一个不透明的盒子里有完全相同的三个小球,球上分别标有数字“
在这次数学知识竟赛中有这样一道题:一个不透明的盒子里有完全相同的三个小球,球上分别标有数字“![]() ”,“
”,“![]() ”和“2”,随机摸出一个小球,把小球上的数字记为x放回后再随机摸出一个小球,把小球上的数字记为y,把x作为横坐标,把y作为纵坐标,记作点
”和“2”,随机摸出一个小球,把小球上的数字记为x放回后再随机摸出一个小球,把小球上的数字记为y,把x作为横坐标,把y作为纵坐标,记作点![]() 用列表法或树状图法求这个点在第二象限的概率.
用列表法或树状图法求这个点在第二象限的概率.