题目内容
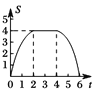
【题目】已知：过
外一点C作
直径AF，垂足为E，交弦AB于D，若
，则
判断直线BC与的位置关系，并证明；
为OA中点，
，
，请直接写出图中阴影部分的面积．
【答案】（1）直线BC与
相切，理由见解析；（2）
【解析】
（1）相切，根据等腰三角形的性质及对顶角相等可得：∠ADE=∠CDB=∠CBD，由直角三角形的两锐角互余可得结论；
（2）先根据直角三角形30度角的性质和勾股定理得：ED=
AD=2，AE=2
，则半径OA=OB=4，作辅助线，证明OM⊥AB和△CDB是等边三角形，根据S阴影=S四边形OECB-S△OEM-S扇形OMB，代入可得结论．
直线BC与相切，
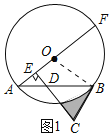
证明：连接OB，
，
，
，
，
，
，
，
，
，
，
是半径，
直线BC与相切；
中，
，
，
，
由勾股定理得：
，
为OA中点，
，
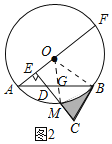
设EC交于M，连接OM，交AB于G，
中，
，
，
，
，
，
，
，
，
，
，
，
，
，
，
，
，
，
是等边三角形，
，
，
，
，
，
练习册系列答案
小学教材完全解读系列答案
相关题目
【题目】小明根据学习函数的经验，对函数y=
-5x+4 的图象与性质进行了探究．下面是小明的探究过程，请补充完整：
（1）自变量x的取值范围是全体实数，x与y的几组对应数值如下表：
x | … |
|
| -2 |
|
| -1 |
|
| 0 |
|
| 1 |
|
| 2 |
| td style="width:17.7pt; border-right-style:solid; border-right-width:0.75pt; border-left-style:solid; border-left-width:0.75pt; border-bottom-style:solid; border-bottom-width:0.75pt; padding:3.38pt 5.03pt; vertical-align:middle">… | |
y | … | 4.3 | 3.2 | 0 | -2.2 | -1.4 | 0 | 2.8 | 3.7 | 4 | 3.7 | 2.8 | 0 | -1.4 | -2.2 | m | 3.2 | 4.3 | … |
其中m= ；
（2）如图，在平面直角坐标系xOy中，描出了以上表中各组对应值为坐标的点，根据描出的点，画出该函数的图象；
（3）观察函数图象，写出一条该函数的性质 ；
（4）进一步探究函数图象发现：
①方程
有 个互不相等的实数根；
②有两个点（x1，y1）和（x2，y2）在此函数图象上，当x2 >x1>2时，比较y1和y2的大小关系为：
y1 y2 (填“>”、“<”或“=”) ；
③若关于x的方程
有4个互不相等的实数根，则a的取值范围是 .
