Question

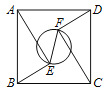
【题目】如图，正方形ABCD中，AD＝5，点E、F是正方形ABCD内的两点，且AE＝FC＝4，BE＝DF＝3，则以EF为直径的圆的面积为( )

A. B. C. D.

Answer 1

【答案】A

【解析】如图，延长DF交AE于点M，

∵正方形ABCD中，AD=AB=DC=5，AE=FC=4，BE=DF=3，

∴△ABE≌△CDF（SSS），AB2=AE2+BE2，CD2=FC2+DF2，

∴∠AEB=∠CFD=90°，∠BAE=∠DCF，

∴∠BAE+∠ABE=∠BAE+∠DAM=90°，∠DCF+∠CDF=∠ADF+∠CDF=90°，

∴∠ABE=∠DAM，∠ADF=∠DCF=∠BAE，

又∵AB=AD，

∴△ABE≌△DAM（ASA），

∴AM=BE=3，DM=AE=4，∠AMD=∠BEA=90°，

∴ME=AE-AM=4-3-1，MF=DM-DF=4-3=1，∠DME=90°，

∴EF=，

∴以EF为直径的圆的面积为： .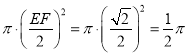

故选A.