题目内容
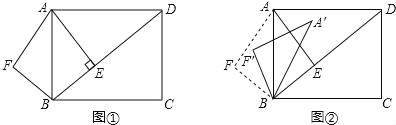
【题目】已知:如图①,在矩形ABCD中,AB=5,AD=![]() ,AE⊥BD,垂足是E.点F是点E关于AB的对称点,连接AF、BF.
,AE⊥BD,垂足是E.点F是点E关于AB的对称点,连接AF、BF.
(1)求AE和BE的长;
(2)若将△ABF沿着射线BD方向平移,设平移的距离为m(平移距离指点B沿BD方向所经过的线段长度).当点F分别平移到线段AB、AD上时,直接写出相应的m的值;
(3)如图②,将△ABF绕点B顺时针旋转一个角α(0°<α<180°),记旋转中的△ABF为△A′BF′,在旋转过程中,设A′F′所在的直线与直线AD交于点P.与直线BD交于点Q.是否存在这样的P、Q两点,使△DPQ为等腰三角形?若存在,求出此时DQ的长;若不存在,请说明理由.
【答案】(1)AE=4 ;BE=3;(2)3;![]() ;(3)
;(3)![]() 或
或![]() 或
或![]() 或
或![]() .
.
【解析】
试题分析:(1)利用矩形性质、勾股定理及三角形面积公式求解;
(2)依题意画出图形,如答图2所示.利用平移性质,确定图形中的等腰三角形,分别求出m的值;
(3)在旋转过程中,等腰△DPQ有4种情形,如答图3所示,对于各种情形分别进行计算.
试题解析:(1)在Rt△ABD中,AB=5,AD=![]() ,
,
由勾股定理得:BD=![]() =
=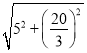 =
=![]() .
.
∵![]() =
=![]() BDAE=
BDAE=![]() ABAD,
ABAD,
∴AE= =4.
=4.
在Rt△ABE中,AB=5,AE=4,
由勾股定理得:BE=3;
(2)设平移中的三角形为△A′B′F′,如答图2所示:
由对称点性质可知,∠1=∠2.
由平移性质可知,AB∥A′B′,∠4=∠1,BF=B′F′=3.

①当点F′落在AB上时,
∵AB∥A′B′,
∴∠3=∠4,
∴∠3=∠2,
∴BB′=B′F′=3,即m=3;
②当点F′落在AD上时,
∵AB∥A′B′,
∴∠6=∠2,
∵∠1=∠2,∠5=∠1,
∴∠5=∠6,
又易知A′B′⊥AD,
∴△B′F′D为等腰三角形,
∴B′D=B′F′=3,
∴BB′=BD﹣B′D=![]() ﹣3=
﹣3=![]() ,即m=
,即m=![]() ;
;
(3)存在.理由如下:
在旋转过程中,等腰△DPQ依次有以下4种情形:
①如答图3﹣1所示,点Q落在BD延长线上,且PD=DQ,易知∠2=2∠Q,

∵∠1=∠3+∠Q,∠1=∠2,
∴∠3=∠Q,
∴A′Q=A′B=5,
∴F′Q=F′A′+A′Q=4+5=9.
在Rt△BF′Q中,由勾股定理得:BQ=![]() =img src="http://thumb.zyjl.cn/questionBank/Upload/2017/12/28/22/bdbb4804/SYS201712282241170911399810_DA/SYS201712282241170911399810_DA.017.png" width="39" height="24" style="-aw-left-pos:0pt; -aw-rel-hpos:column; -aw-rel-vpos:paragraph; -aw-top-pos:0pt; -aw-wrap-type:inline" />.
=img src="http://thumb.zyjl.cn/questionBank/Upload/2017/12/28/22/bdbb4804/SYS201712282241170911399810_DA/SYS201712282241170911399810_DA.017.png" width="39" height="24" style="-aw-left-pos:0pt; -aw-rel-hpos:column; -aw-rel-vpos:paragraph; -aw-top-pos:0pt; -aw-wrap-type:inline" />.
∴DQ=BQ﹣BD=![]() ;
;
②如答图3﹣2所示,点Q落在BD上,且PQ=DQ,易知∠2=∠P,
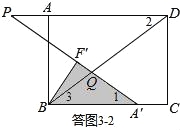
∵∠1=∠2,
∴∠1=∠P,
∴BA′∥PD,则此时点A′落在BC边上.
∵∠3=∠2,
∴∠3=∠1,
∴BQ=A′Q,
∴F′Q=F′A′﹣A′Q=4﹣BQ.
在Rt△BQF′中,由勾股定理得:![]() ,
,
即![]() ,
,
解得:BQ=![]() ,
,
∴DQ=BD﹣BQ=![]() =
=![]() ;
;
③如答图3﹣3所示,点Q落在BD上,且PD=DQ,易知∠3=∠4.

∵∠2+∠3+∠4=180°,∠3=∠4,
∴∠4=90°﹣![]() ∠2.
∠2.
∵∠1=∠2,
∴∠4=90°﹣![]() ∠1.
∠1.
∴∠A′QB=∠4=90°﹣![]() ∠1,
∠1,
∴∠A′BQ=180°﹣∠A′QB﹣∠1=90°﹣![]() ∠1,
∠1,
∴∠A′QB=∠A′BQ,
∴A′Q=A′B=5,
∴F′Q=A′Q﹣A′F′=5﹣4=1.
在Rt△BF′Q中,由勾股定理得:BQ=![]() =
=![]() ,
,
∴DQ=BD﹣BQ=![]() ;
;
④如答图3﹣4所示,点Q落在BD上,且PQ=PD,易知∠2=∠3.

∵∠1=∠2,∠3=∠4,∠2=∠3,
∴∠1=∠4,
∴BQ=BA′=5,
∴DQ=BD﹣BQ=![]() ﹣5=
﹣5=![]() .
.
综上所述,存在4组符合条件的点P、点Q,使△DPQ为等腰三角形;
DQ的长度分别为![]() 或
或![]() 或
或![]() 或
或![]() .
.

 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案