题目内容
【题目】如图1，在平面直角坐标系中，矩形OABC的顶点O在坐标原点，顶点A、C分别在x轴、y轴的正半轴上，且OA=2，OC=1，矩形对角线AC、OB相交于E，过点E的直线与边OA、BC分别相交于点G、H． 
（1）直接写出点E的坐标： ．
（2）求证：AG=CH．
（3）如图2，以O为圆心，OC为半径的圆弧交OA与D，若直线GH与弧CD所在的圆相切于矩形内一点F，求直线GH的函数关系式． 
（4）在（3）的结论下，梯形ABHG的内部有一点P，当⊙P与HG、GA、AB都相切时，求⊙P的半径．
【答案】
（1）（1， 
）
（2）解：证明：∵矩形OABC，
∴CE=AE，BC∥OA，
∴∠HCE=∠EAG，
∵在△CHE和△AGE中
，
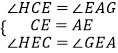∴△CHE≌△AGE，
∴AG=CH
（3）解：解：如图2，连接DE并延长DE交CB于M，连接AC，
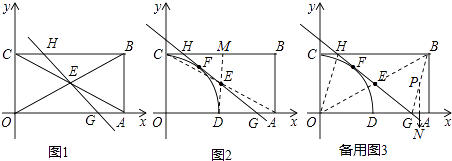
∵DO=OC=1= OA，
∴D是OA的中点，
∵BC∥OA，
∴∠MCE=∠DAE，
∵在△CME和△ADE中
，
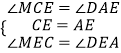∴△CME≌△ADE，
∴CM=AD=2﹣1=1，
∵四边形OABC是矩形，
∴∠MCO=∠COD=90°，CB∥OA，
∵OD=1，OA=2，
∴OD=AD，
∵矩形OABC的对角线交于E，
∴E为中心，
∴DE∥OC，
∴四边形CMDO是矩形，
∴MD⊥OD，MD⊥CB，
∴MD切⊙O于D，
∵HG切⊙O于F，E（1， ），
∴可设CH=HF=x，FE=ED= MD，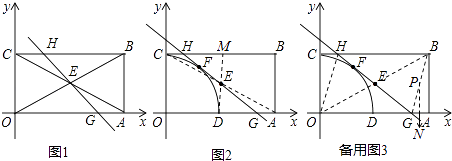 
在Rt△MHE中，有MH2+ME2=HE2，
即（1﹣x）2+（ ）2=（ +x）2，
解得x= 
，
∴H（ ，1），OG=2﹣ = 
，
∴G（ ，0），
设直线GH的解析式是：y=kx+b，
把G、H的坐标代入得： k+b=0，且1= k+b，
解得：k=﹣ 
，b= 
，
∴直线GH的函数关系式为y=﹣ x+
（4）解：解：如备用图3，连接BG，过P做PN⊥GA，垂足为N，
∵在△OCH和△BAG中
，
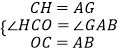∴△OCH≌△BAG，
∴∠CHO=∠AGB，
∵∠HCO=90°，
∴HC切⊙O于C，HG切⊙O于F，
∴OH平分∠CHF，
∴∠CHO=∠FHO=∠BGA，
∵四边形OCBA是矩形，
∴BC∥OA，BC=OA，
∵CH=AG（已证），
∴BH=OG，BH∥OG，
∴四边形BHOG是平行四边形，
∴OH∥BG，
∴∠OHE=∠BGE，
∵∠CHO=∠FHO=∠BGA
∴∠BGA=∠BGE，
即BG平分∠FGA，
∵⊙P与HG、GA、AB都相切，
∴和∠HGA的两边都相切的圆的圆心在∠HGA的角平分线上，即在GB上
∴圆心P必在BG上，
∴△GPN∽△GBA，
∴ 
，
设半径为r，
= 
，
解得：r= 
．
答：⊙P的半径是
【解析】（1）解：E的坐标是：（1， ）， 所以答案是：（1， ）；
【考点精析】解答此题的关键在于理解勾股定理的概念的相关知识，掌握直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2，以及对矩形的性质的理解，了解矩形的四个角都是直角，矩形的对角线相等．
