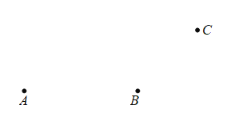题目内容
【题目】如图,![]() 是线段
是线段![]() 上一点,
上一点,![]() ,
,![]() 、
、![]() 两点分别从
两点分别从![]() 、
、![]() 出发以
出发以![]() 、
、![]() 的速度沿直线
的速度沿直线![]() 向左运动(
向左运动(![]() 在线段
在线段![]() 上,
上,![]() 在线段
在线段![]() 上),运动的时间为
上),运动的时间为![]() .
.

(1)当![]() 时,
时,![]() ,请求出
,请求出![]() 的长;
的长;
(2)当![]() 时,
时,![]() ,请求出
,请求出![]() 的长;
的长;
(3)若![]() 、
、![]() 运动到任一时刻时,总有
运动到任一时刻时,总有![]() ,请求出
,请求出![]() 的长;
的长;
(4)在(3)的条件下,![]() 是直线
是直线![]() 上一点,且
上一点,且![]() ,求
,求![]() 的长.
的长.
【答案】(1)4cm;(2)4cm;(3)4cm;(4)4cm或12cm.
【解析】
(1)(2)根据C、D的运动速度知BD=2PC,再由已知条件PD=2AC求得PB=2AP,由此求得AP的值;
(3)结合(1)、(2)进行解答;
(4)由题设画出图示,根据AQBQ=PQ求得AQ=PQ+BQ;然后求得AP=BQ,从而求得PQ与AB的关系.
解:(1)因为点C从P出发以1(cm/s)的速度运动,运动的时间为t=1(s),
所以![]() (cm).
(cm).
因为点D从B出发以2(cm/s)的速度运动,运动的时间为t=1(s),
所以![]() (cm).
(cm).
故BD=2PC.
因为PD=2AC,BD=2PC,
所以BD+PD=2(PC+AC),即PB=2AP.
故AB=AP+PB=3AP.
因为AB=12cm,
所以![]() (cm).
(cm).
![]()
(2)因为点C从P出发以1(cm/s)的速度运动,运动的时间为t=2(s),
所以PC=![]() (cm)
(cm)
因为点D从B出发以2(cm/s)的速度运动,运动的时间为t=2(s),
所以BD=![]() (cm)
(cm)
故BD=2PC
因为PD=2AC,BD=2PC,
所以BD+PD=2(PC+AC),即PB=2AP
故AB=AP+PB=3AP
因为AB=12cm,所以AP=![]() cm
cm
(3)因为点C从P出发以1(cm/s)的速度运动,运动的时间为t(s),
所以![]() (cm).
(cm).
因为点D从B出发以2(cm/s)的速度运动,运动的时间为t(s),
所以![]() (cm).
(cm).
故BD=2PC.
因为PD=2AC,BD=2PC,
所以BD+PD=2(PC+AC),即PB=2AP.
故AB=AP+PB=3AP.
因为AB=12cm,
所以![]() (cm).
(cm).
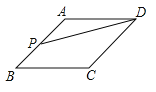
(4)本题需要对以下两种情况分别进行讨论.
![]()
![]()
① ②
(1)点Q在线段AB上(如图①).
因为AQ-BQ=PQ,所以AQ=PQ+BQ.
因为AQ=AP+PQ,所以AP=BQ.
因为![]() ,所以
,所以![]() .
.
故![]() .
.
因为AB=12cm,所以![]() (cm).
(cm).
(2)点Q不在线段AB上,则点Q在线段AB的延长线上(如图②).
因为AQ-BQ=PQ,所以AQ=PQ+BQ.
因为AQ=AP+PQ,所以AP=BQ.
因为![]() ,所以
,所以![]() .
.
故![]() .
.
因为AB=12cm,所以![]() (cm).
(cm).
综上所述,PQ的长为4cm或12cm.

【题目】佳乐家超市元旦期间搞促销活动,活动方案如下表:
一次性购物 | 优惠方案 |
不超过200元 | 不给予优惠 |
超过200元,而不超过1000元 | 优惠10% |
超过1000元 | 其中1000元按8.5折优惠,超过部分按7折优惠 |
小颖在促销活动期间两次购物分别支付了134元和913元.
(1)小颖两次购买的物品如果不打折,应支付多少钱?
(2)在此活动中,他节省了多少钱?