题目内容
【题目】在平面直角坐标系xOy中,二次函数C1:![]() (m>0)的图象与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C.
(m>0)的图象与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C.
(1)求点A和点C的坐标;
(2)当AB=4时,
①求二次函数C1的表达式;
②在抛物线的对称轴上是否存在点D,使△DAC的周长最小,若存在,求出点D的坐标,若不存在,请说明理由;
(3)将(2)中抛物线C1向上平移n个单位,得到抛物线C2,若当0≤x≤![]() 时,抛物线C2与x轴只有一个公共点,结合函数图象,求出n的取值范围.
时,抛物线C2与x轴只有一个公共点,结合函数图象,求出n的取值范围.
【答案】(1)A(-1,0);C(0,-3);(2)①![]() ;② D(1,-2);(3)
;② D(1,-2);(3)![]() ≤n<3或n=4.
≤n<3或n=4.
【解析】
(1)解方程![]() 即可得到点A、B的坐标;在函数
即可得到点A、B的坐标;在函数![]() 中,由x=0可得y=-3,由此可得点C的坐标;
中,由x=0可得y=-3,由此可得点C的坐标;
(2)①由(1)中所得点A、B的坐标结合AB=4可得m的值,由此即可得到函数的解析式;②由题意可知,AC是定值,而A、B两点关于抛物线的对称轴对称,由此可知当点D为直线BC与抛物线的对称轴的交点时,△ACD的周长最小,故由已知条件求得直线BC的解析式,再求出BC与对称轴的交点的坐标即可;
(3)①由题意设平移后的抛物线C2的解析式为:![]() ,当平移后的抛物线过点(
,当平移后的抛物线过点(![]() ,0)和(0,0)时,由抛物线的对称轴为直线x=1可得抛物线与x轴的另一个交点为(-0.5,0)和(1,0),由点(-0.5,0)不在
,0)和(0,0)时,由抛物线的对称轴为直线x=1可得抛物线与x轴的另一个交点为(-0.5,0)和(1,0),由点(-0.5,0)不在![]() 的范围内,点(1,0)在
的范围内,点(1,0)在![]() 可求得n的一个符合题意的取值范围; ②当平移后的抛物线
可求得n的一个符合题意的取值范围; ②当平移后的抛物线![]() 的顶点在x轴上时,新抛物线与x轴也只有一个交点(1,0)在
的顶点在x轴上时,新抛物线与x轴也只有一个交点(1,0)在![]() 的范围内,由此也可得到一个符合条件的n的值;综合①②即可得到n的取值范围.
的范围内,由此也可得到一个符合条件的n的值;综合①②即可得到n的取值范围.
(1)在二次函数![]() 中,当y=0时,可得方程:
中,当y=0时,可得方程:
![]() ,
,
解得:![]() ,
,
∵抛物线![]() 与x轴的交点A在点B的左侧,且m>0,
与x轴的交点A在点B的左侧,且m>0,
∴点A的坐标为(-1,0),点B的坐标为(![]() ,0),
,0),
∵在![]() 中,当x=0时,y=-3,
中,当x=0时,y=-3,
∴点C的坐标为(0,-3);
(2)①∵点A的坐标为(-1,0),点B的坐标为(![]() ,0),且m>0,
,0),且m>0,
∴AB=![]() +1,
+1,
又∵AB=4,
∴![]() +1=4,解得m=1,
+1=4,解得m=1,
∴抛物线的解析式为:![]() ;
;
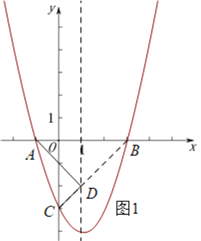
②如图1,由m=1,可得点B的坐标为(3,0),
∵AC的长为定值,A、B两点关于抛物线的对称轴x=1对称,
∴当点D为直线BC与对称轴x=1的交点时,AD+CD最小,此时△ACD的周长最小,
∵点B的坐标为(3,0),点C的坐标为(0,-3),
∴直线BC的表达式为 y=x-3.
把x=1代入y=x-3得y=-2,
∴D(1,-2);
(3)设抛物线C2的表达式为![]()
①当抛物线C2经过点(![]() ,0)时,解得:n =
,0)时,解得:n =![]() ,此时抛物线与x轴的另一个交点为(-0.5,0),该点不在
,此时抛物线与x轴的另一个交点为(-0.5,0),该点不在![]() 范围内;
范围内;
当抛物线C2经过点(0,0)时,解得得n=3,此时抛物线与x轴的另一个交点为(1,0),该点在![]() 的范围内,
的范围内,
∴综上可得:![]() ≤n<3 ;
≤n<3 ;
②当抛物线![]() 的顶点在x轴上时,抛物线C2与x轴只有一个公共点,此时有x=1,y=0,解得n=4;
的顶点在x轴上时,抛物线C2与x轴只有一个公共点,此时有x=1,y=0,解得n=4;
综合①②可得,n的取值范围是![]() ≤n<3或n=4.
≤n<3或n=4.

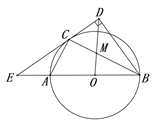
【题目】如图,在![]() 中,
中,![]() 是
是![]() 的中点,
的中点,![]() 是边
是边![]() 上一动点,连结
上一动点,连结![]() ,取
,取![]() 的中点
的中点![]() ,连结
,连结![]() .小梦根据学习函数的经验,对
.小梦根据学习函数的经验,对![]() 的面积与
的面积与![]() 的长度之间的关系进行了探究:
的长度之间的关系进行了探究:

(1)设![]() 的长度为
的长度为![]() ,
,![]() 的面积
的面积![]() ,通过取
,通过取![]() 边上的不同位置的点
边上的不同位置的点![]() ,经分析和计算,得到了
,经分析和计算,得到了![]() 与
与![]() 的几组值,如下表:
的几组值,如下表:
| 0 | 1 | 2 | 3 | 4 | 5 | 6 |
| 3 |
| 1 | 0 |
| 2 | 3 |
根据上表可知,![]() ______,
______,![]() ______.
______.
(2)在平面直角坐标系![]() 中,画出(1)中所确定的函数的图象.
中,画出(1)中所确定的函数的图象.

(3)在(1)的条件下,令![]() 的面积为
的面积为![]() .
.
①用![]() 的代数式表示
的代数式表示![]() .
.
②结合函数图象.解决问题:当![]() 时,
时,![]() 的取值范围为______.
的取值范围为______.