��Ŀ����
����Ŀ������������⣺
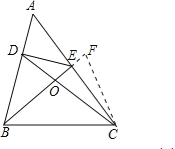
��ͼ������ABC�У���A����ǣ���D��E�ֱ���AB��AC�ϣ���![]() ��BE��CD�ཻ�ڵ�O��̽��BD��CE֮���������ϵ����֤����Ľ��ۣ�
��BE��CD�ཻ�ڵ�O��̽��BD��CE֮���������ϵ����֤����Ľ��ۣ�

С��ͬѧ������˼���ģ�
��ƽʱ��ѧϰ�У��������ľ��飺������ABC�ǵ��������Σ���ô�ڸ���һ���Ӧ��������ͼa��BE��CD�ֱ������ǵ�ƽ������������ͼb��BE��CD�ֱ����������ĸ��ߣ�������ͼc��BE��CD�ֱ�����������������ʱ������ͼ�ε���Գ��ԣ�����ȫ�������κ͵��������ε��й�֪ʶ�Ϳ�֤�ø�����ȵ��߶λ���ȵĽ�.�������Ҳ������ͨ�����Ӹ����߹�����Գ�ͼ���������

ͼa ͼb ͼc
��ο�С��ͬѧ��˼·���������������⣮.
���𰸡�BD=CE�����ɼ�����.
��������
�����������CΪ��������FCB=��DBC��CF��BE��F�㣬����֤����BDC�ա�CFB���Ϳ��Եó�BD=CF����BDC=��CFB�������ó���CFB=��CEF�Ϳ��Եó�CE=CF���ó����ۣ�
�������: BD=CE���������£�
��ͼ����CΪ��������FCB=��DBC��CF��BE��F�㣮
����BDC����CFB��
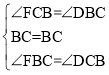 ��
��
���BDC�ա�CFB��SAS����
��BD=CF����BDC=��CFB��
�ߡ�DCB=��EBC=![]() ��A��
��A��
���DCB+��EBC=��A��
�ߡ�DCB+��EBC=��FOC��
���FOC=��A��
�ߡ�BDC=��A+��ACD��
���CFB=��A+��ACD��
���CFB=��FOC+��ACD��
�ߡ�FEC=��FOC+��ACD��
���CFB=��CEF��
��CE=CF��
��BD=CE��
����: 1.ȫ�������ε��ж������ʣ�2.���������ε����ʣ�3.��ԳƵ�����.

 �ƸԺ���ȫ�����Ų��Ծ�ϵ�д�
�ƸԺ���ȫ�����Ų��Ծ�ϵ�д�

