题目内容
【题目】如图,△ABC内接于⊙O,BC是直径,⊙O的切线PA交CB的延长线于点P,OE∥AC交AB于点F,交PA于点E,连接BE.
(1)判断BE与⊙O的位置关系并说明理由;
(2)若⊙O的半径为4,BE=3,求AB的长.

【答案】(1)BE是⊙O的切线;(2)![]() .
.
【解析】试题分析:(1)结论:BE是⊙O的切线.首先证明∠OAP=90°,再证明△EOB≌△EOA,推出∠OBE=∠OAE即可解决问题.
(2)由(1)可知AB=2BF,在Rt△BEO中,∠OBE=90°,OB=4,BE=3,可得OE=![]() =5,由
=5,由![]() BEOB=
BEOB=![]() OEBF,可得BF=
OEBF,可得BF=![]() =
=![]() ,由此即可解决问题.
,由此即可解决问题.
试题解析:(1)BE是⊙O的切线.
理由:如图连接OA.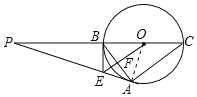
∵PA是切线,
∴PA⊥OA,
∴∠OAP=90°,
∵BC是直径,
∴∠BAC=90°,
∵OE∥AC,
∴∠OFB=∠BAC=90°,
∴OE⊥AB,
∴BF=FA,
∵OB=OA,
∴∠EOB=∠EOA,
在△EOB和△EOA中,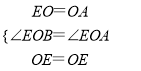 ,
,
∴△EOB≌△EOA,
∴∠OBE=∠OAE=90°,
∴OB⊥BE,
∴BE是⊙O的切线.
(2)由(1)可知AB=2BF,
在Rt△BEO中,∵∠OBE=90°,OB=8,BE=6,
∴OE=![]() =5,
=5,
∵![]() BEOB=
BEOB=![]() OEBF,
OEBF,
∴BF=![]() =
=![]() ,
,
∴AB=2BF=![]()
.

练习册系列答案
相关题目
【题目】某自行车厂计划一周生产自行车2100辆,平均每天计制生产300辆,实际每天生产量与计划量相比有出入,下表是某周的生产情况.(超过每天计划生产数记为正,不足每天计划生产数记为负)
星期 | 一 | 二 | 三 | 四 | 五 | 六 | 日 |
每天超出计划的量数 |
|
|
|
|
|
|
|
(1)该厂星期四实际生产自行车______辆
(2)该厂本周实际每天平均生产多少辆自行车?