Question

【题目】已知直线AB∥CD,将一块三角板EFG如图1所示,△EFG的边与直线AB、CD分别相交于M,N两点，∠F=90°，∠E=30°.

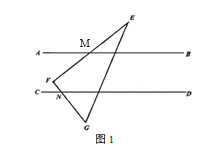
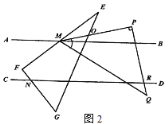
(1)求证:∠EMB+∠DNG=90°

(2)将另一块三角板MPQ如图2放置,△MPQ的边PQ、PM分别与直线CD相交于点R,与△EFG的EG相交于点O,∠P=90°,∠PMQ=45°,直接写出∠PMB与∠PRD的数量关系:

Answer 1

【答案】（1）见解析（2）∠PMB+90°=∠PRD.

【解析】

（1）过点F作FH∥AB,即FH∥CD，再根据平行线的关系得到∠EMB+∠DNG=∠EFG，即可求解；

（2）根据平行线的性质及三角形的外角定理即可求解；

（1）过点F作FH∥AB,即FH∥CD，

∴∠EMB=∠EFH，∠DNG=∠HFG

∴∠EMB+∠DNG=∠EFG=90°；

（2）∠PMB+90°=∠PRD，理由如下：

设AB与PQ交于K点，

∵AB∥CD，

∴∠PRD=∠PKB，

∵∠PKB是△PMK的一个外角，

∴∠PMB+90°=∠PKB

故∠PMB+90°=∠PRD，