题目内容
如图,在△ABC中,BE、CD相交于点O,BE=CD,∠BDC=∠CEB.求证:△ABC是等腰三角形.
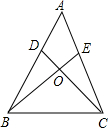

证明:∵∠BDC=∠CEB,
∴∠ADC=∠AEB,
在△AEB和△ADC中,
,
∴△AEB≌△ADC(AAS),
∴AB=AC,
∴△ABC是等腰三角形.
∴∠ADC=∠AEB,
在△AEB和△ADC中,
|
∴△AEB≌△ADC(AAS),
∴AB=AC,
∴△ABC是等腰三角形.

练习册系列答案
相关题目