题目内容
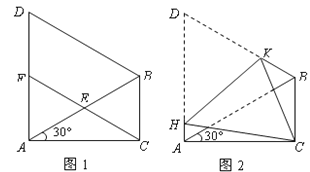
【题目】如图1,在Rt△ACB中,∠ACB=90°,AC=3,BC=4,有一过点C的动圆⊙O与斜边AB相切于动点P,连接CP.
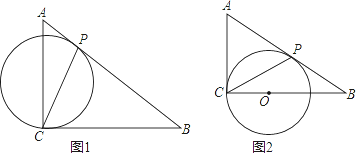
(1)当⊙O与直角边AC相切时,如图2所示,求此时⊙O的半径r的长;
(2)随着切点P的位置不同,弦CP的长也会发生变化,试求出弦CP的长的取值范围.
(3)当切点P在何处时,⊙O的半径r有最大值?试求出这个最大值.
【答案】(1) r=![]() ;(2)
;(2) ![]() ≤PC≤4;(3)
≤PC≤4;(3) ![]() .
.
【解析】
试题分析:(1)先根据勾股定理求出AB的长,再由切线的性质求出PB的长,过P作PQ⊥BC于Q,过O作OR⊥PC于R,根据PQ∥AC得出PC的长,再由△COR∽△CPQ即可得出r的值;
(2)根据最短PC为AB边上的高,最大PC=BC=4即可得出结论;
(3)当P与B重合时,圆最大.这时,O在BD的垂直平分线上,过O作OD⊥BC于D,由BD=![]() BC=2,由于AB是切线可知∠ABO=90°,∠ABD+∠OBD=∠BOD+∠OBD=90°,故可得出∠ABC=∠BOD,根据锐角三角函数的定义即可得出结论.
BC=2,由于AB是切线可知∠ABO=90°,∠ABD+∠OBD=∠BOD+∠OBD=90°,故可得出∠ABC=∠BOD,根据锐角三角函数的定义即可得出结论.
试题解析:(1)如图1,

∵在Rt△ACB中,∠ACB=90°,AC=3,BC=4,
∴AB=![]() .
.
∵AC、AP都是圆的,圆心在BC上,AP=AC=3,
∴PB=2,
过P作PQ⊥BC于Q,过O作OR⊥PC于R,
∵PQ∥AC,
∴![]() ,
,
∴PQ=![]() ,BQ=
,BQ=![]() ,
,
∴CQ=BC-BQ=![]() ,
,
∴PC=![]() ,
,
∵点O是CE的中点,
∴CR=![]() PC=
PC=![]() ,
,
∴∠PCE=∠PCE,∠CRO=∠CQP,
∴△COR∽△CPQ,
∴![]() ,即
,即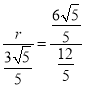 ,解得r=
,解得r=![]() ;
;
(2)∵最短PC为AB边上的高,即PC=![]() =
=![]() ,最大PC=BC=4,
,最大PC=BC=4,
∴![]() ≤PC≤4;
≤PC≤4;

(3)如图2,当P与B重合时,圆最大.O在BD的垂直平分线上,过O作OD⊥BC于D,由BD=![]() BC=2,
BC=2,
∵AB是切线,
∴∠ABO=90°,
∴∠ABD+∠OBD=∠BOD+∠OBD=90°,
∴∠ABC=∠BOD,
∴![]() =sin∠BOD=sin∠ABC=
=sin∠BOD=sin∠ABC=![]() ,
,
∴OB=![]() ,即半径最大值为
,即半径最大值为![]() .
.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案