ΧβΡΩΡΎ»ί
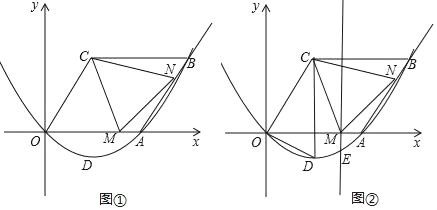
ΓΨΧβΡΩΓΩ»γΆΦ≈ΉΈοœΏy=ax2+bxΘ§ΙΐΒψAΘ®4Θ§0Θ©ΚΆΒψBΘ®6Θ§2![]() Θ©Θ§ΥΡ±Ώ–ΈOCBA «ΤΫ––ΥΡ±Ώ–ΈΘ§ΒψMΘ®tΘ§0Θ©ΈΣx÷α’ΐΑκ÷α…œΒΡΒψΘ§ΒψNΈΣ…δœΏAB…œΒΡΒψΘ§«“AN=OMΘ§ΒψDΈΣ≈ΉΈοœΏΒΡΕΞΒψΘ°
Θ©Θ§ΥΡ±Ώ–ΈOCBA «ΤΫ––ΥΡ±Ώ–ΈΘ§ΒψMΘ®tΘ§0Θ©ΈΣx÷α’ΐΑκ÷α…œΒΡΒψΘ§ΒψNΈΣ…δœΏAB…œΒΡΒψΘ§«“AN=OMΘ§ΒψDΈΣ≈ΉΈοœΏΒΡΕΞΒψΘ°
Θ®1Θ©«σ≈ΉΈοœΏΒΡΫβΈω ΫΘ§≤Δ÷±Ϋ”–¥≥ωΒψDΒΡΉχ±ξΘΜ
Θ®2Θ©Β±ΓςAMNΒΡ÷ή≥ΛΉν–Γ ±Θ§«σtΒΡ÷ΒΘΜ
Θ®3Θ©»γΆΦΔΎΘ§ΙΐΒψMΉςMEΓΆx÷αΘ§ΫΜ≈ΉΈοœΏy=ax2+bx”ΎΒψEΘ§Ν§Ϋ”EMΘ§AEΘ§Β±ΓςAME”κΓςDOCœύΥΤ ±Θ°«κ÷±Ϋ”–¥≥ωΥυ”–ΖϊΚœΧθΦΰΒΡΒψMΉχ±ξΘ°
ΓΨ¥πΑΗΓΩΘ®1Θ©y=![]() x2©¹
x2©¹![]() xΘ§ΒψDΒΡΉχ±ξΈΣΘ®2Θ§©¹
xΘ§ΒψDΒΡΉχ±ξΈΣΘ®2Θ§©¹![]() Θ©ΘΜΘ®2Θ©t=2ΘΜΘ®3Θ©MΒψΒΡΉχ±ξΈΣΘ®2Θ§0Θ©ΜρΘ®6Θ§0Θ©Θ°
Θ©ΘΜΘ®2Θ©t=2ΘΜΘ®3Θ©MΒψΒΡΉχ±ξΈΣΘ®2Θ§0Θ©ΜρΘ®6Θ§0Θ©Θ°
ΓΨΫβΈωΓΩ
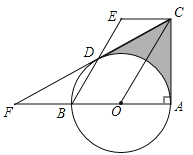
Θ®1Θ©άϊ”Ο¥ΐΕ®œΒ ΐΖ®«σ≈ΉΈοœΏΫβΈω ΫΘΜάϊ”Ο≈δΖΫΖ®Α―“ΜΑψ ΫΜ·ΈΣΕΞΒψ ΫΒΟΒΫΒψDΒΡΉχ±ξΘΜ
Θ®2Θ©Ν§Ϋ”ACΘ§»γΆΦΔΌΘ§œ»ΦΤΥψ≥ωAB=4Θ§‘ρ≈–ΕœΤΫ––ΥΡ±Ώ–ΈOCBAΈΣΝβ–ΈΘ§‘Ό÷ΛΟςΓςAOCΚΆΓςACBΕΦ «Β»±Ώ»ΐΫ«–ΈΘ§Ϋ”Ή≈÷ΛΟςΓςOCMΓ’ΓςACNΒΟΒΫCM=CNΘ§ΓœOCM=ΓœACNΘ§‘ρ≈–ΕœΓςCMNΈΣΒ»±Ώ»ΐΫ«–ΈΒΟΒΫMN=CMΘ§”Ύ «ΓςAMNΒΡ÷ή≥Λ=OA+CMΘ§”…”ΎCMΓΆOA ±Θ§CMΒΡ÷ΒΉν–ΓΘ§ΓςAMNΒΡ÷ή≥ΛΉν–ΓΘ§¥”ΕχΒΟΒΫtΒΡ÷ΒΘΜ
Θ®3Θ©œ»άϊ”ΟΙ¥Ι…Ε®άμΒΡΡφΕ®άμ÷ΛΟςΓςOCDΈΣ÷±Ϋ«»ΐΫ«–ΈΘ§ΓœCOD=90ΓψΘ§…ηMΘ®tΘ§0Θ©Θ§‘ρEΘ®tΘ§![]() t2-
t2-![]() tΘ©Θ§ΗυΨίœύΥΤ»ΐΫ«–ΈΒΡ≈–Ε®ΖΫΖ®Θ§Β±
tΘ©Θ§ΗυΨίœύΥΤ»ΐΫ«–ΈΒΡ≈–Ε®ΖΫΖ®Θ§Β±![]() ±Θ§ΓςAMEΓΉΓςCODΘ§Φ¥|t-4|ΘΚ4=|
±Θ§ΓςAMEΓΉΓςCODΘ§Φ¥|t-4|ΘΚ4=|![]() t2-
t2-![]() t |ΘΚ
t |ΘΚ![]() Θ§Β±
Θ§Β±![]() ±Θ§ΓςAMEΓΉΓςDOCΘ§Φ¥|t-4|ΘΚ
±Θ§ΓςAMEΓΉΓςDOCΘ§Φ¥|t-4|ΘΚ![]() =|
=|![]() t2-
t2-![]() t |ΘΚ4Θ§»ΜΚσΖ÷±πΫβΨχΕ‘÷ΒΖΫ≥ΧΩ…ΒΟΒΫΕ‘”ΠΒΡMΒψΒΡΉχ±ξΘ°
t |ΘΚ4Θ§»ΜΚσΖ÷±πΫβΨχΕ‘÷ΒΖΫ≥ΧΩ…ΒΟΒΫΕ‘”ΠΒΡMΒψΒΡΉχ±ξΘ°
Θ®1Θ©Α―AΘ®4Θ§0Θ©ΚΆBΘ®6Θ§2![]() Θ©¥ζ»κy=ax2+bxΒΟ
Θ©¥ζ»κy=ax2+bxΒΟ
![]() Θ§ΫβΒΟ
Θ§ΫβΒΟ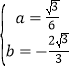 Θ§
Θ§
Γύ≈ΉΈοœΏΫβΈω ΫΈΣy=![]() x2-
x2-![]() xΘΜ
xΘΜ
ΓΏy=![]() x2-
x2-![]() x =
x =![]() -2) 2-
-2) 2-![]() ΘΜ
ΘΜ
ΓύΒψDΒΡΉχ±ξΈΣΘ®2Θ§-![]() Θ©ΘΜ
Θ©ΘΜ
Θ®2Θ©Ν§Ϋ”ACΘ§»γΆΦΔΌΘ§

AB=![]() =4Θ§
=4Θ§
ΕχOA=4Θ§
ΓύΤΫ––ΥΡ±Ώ–ΈOCBAΈΣΝβ–ΈΘ§
ΓύOC=BC=4Θ§
ΓύCΘ®2Θ§2![]() Θ©Θ§
Θ©Θ§
ΓύAC=![]() =4Θ§
=4Θ§
ΓύOC=OA=AC=AB=BCΘ§
ΓύΓςAOCΚΆΓςACBΕΦ «Β»±Ώ»ΐΫ«–ΈΘ§
ΓύΓœAOC=ΓœCOB=ΓœOCA=60ΓψΘ§
ΕχOC=ACΘ§OM=ANΘ§
ΓύΓςOCMΓ’ΓςACNΘ§
ΓύCM=CNΘ§ΓœOCM=ΓœACNΘ§
ΓΏΓœOCM+ΓœACM=60ΓψΘ§
ΓύΓœACN+ΓœACM=60ΓψΘ§
ΓύΓςCMNΈΣΒ»±Ώ»ΐΫ«–ΈΘ§
ΓύMN=CMΘ§
ΓύΓςAMNΒΡ÷ή≥Λ=AM+AN+MN=OM+AM+MN=OA+CM=4+CMΘ§
Β±CMΓΆOA ±Θ§CMΒΡ÷ΒΉν–ΓΘ§ΓςAMNΒΡ÷ή≥ΛΉν–ΓΘ§¥Υ ±OM=2Θ§
Γύt=2ΘΜ
Θ®3Θ©ΓΏCΘ®2Θ§2![]() Θ©Θ§DΘ®2Θ§-
Θ©Θ§DΘ®2Θ§-![]() Θ©Θ§
Θ©Θ§
ΓύCD=![]() Θ§
Θ§
ΓΏOD=![]() Θ§OC=4Θ§
Θ§OC=4Θ§
ΓύOD2+OC2=CD2Θ§
ΓύΓςOCDΈΣ÷±Ϋ«»ΐΫ«–ΈΘ§ΓœCOD=90ΓψΘ§
…ηMΘ®tΘ§0Θ©Θ§‘ρEΘ®tΘ§![]() t2-
t2-![]() tΘ©Θ§
tΘ©Θ§
ΓΏΓœAME=ΓœCODΘ§
ΓύΒ±![]() ±Θ§ΓςAMEΓΉΓςCODΘ§Φ¥|t-4|ΘΚ4=|
±Θ§ΓςAMEΓΉΓςCODΘ§Φ¥|t-4|ΘΚ4=|![]() t2-
t2-![]() t |ΘΚ
t |ΘΚ![]() Θ§
Θ§
’ϊάμΒΟ|![]() t2-
t2-![]() t|=
t|=![]() |t-4|Θ§
|t-4|Θ§
ΫβΖΫ≥Χ![]() t2-
t2-![]() t =
t =![]() Θ®t-4Θ©ΒΟt1=4Θ®…α»ΞΘ©Θ§t2=2Θ§¥Υ ±MΒψΉχ±ξΈΣΘ®2Θ§0Θ©ΘΜ
Θ®t-4Θ©ΒΟt1=4Θ®…α»ΞΘ©Θ§t2=2Θ§¥Υ ±MΒψΉχ±ξΈΣΘ®2Θ§0Θ©ΘΜ
ΫβΖΫ≥Χ![]() t2-
t2-![]() t =-
t =-![]() Θ®t-4Θ©ΒΟt1=4Θ®…α»ΞΘ©Θ§t2=-2Θ®…α»ΞΘ©ΘΜ
Θ®t-4Θ©ΒΟt1=4Θ®…α»ΞΘ©Θ§t2=-2Θ®…α»ΞΘ©ΘΜ
Β±![]() ±Θ§ΓςAMEΓΉΓςDOCΘ§Φ¥|t-4|ΘΚ
±Θ§ΓςAMEΓΉΓςDOCΘ§Φ¥|t-4|ΘΚ![]() =|
=|![]() t2-
t2-![]() t |ΘΚ4Θ§’ϊάμΒΟ|
t |ΘΚ4Θ§’ϊάμΒΟ|![]() t2-
t2-![]() t |=|t-4|Θ§
t |=|t-4|Θ§
ΫβΖΫ≥Χ![]() t2-
t2-![]() t =t-4ΒΟt1=4Θ®…α»ΞΘ©Θ§t2=6Θ§¥Υ ±MΒψΉχ±ξΈΣΘ®6Θ§0Θ©ΘΜ
t =t-4ΒΟt1=4Θ®…α»ΞΘ©Θ§t2=6Θ§¥Υ ±MΒψΉχ±ξΈΣΘ®6Θ§0Θ©ΘΜ
ΫβΖΫ≥Χ![]() t2-
t2-![]() t =-Θ®t-4Θ©ΒΟt1=4Θ®…α»ΞΘ©Θ§t2=-6Θ®…α»ΞΘ©ΘΜ
t =-Θ®t-4Θ©ΒΟt1=4Θ®…α»ΞΘ©Θ§t2=-6Θ®…α»ΞΘ©ΘΜ
Ήέ…œΥυ ωΘ§MΒψΒΡΉχ±ξΈΣΘ®2Θ§0Θ©ΜρΘ®6Θ§0Θ©Θ°

 ‘ΡΕΝΩλ≥ΒœΒΝ–¥πΑΗ
‘ΡΕΝΩλ≥ΒœΒΝ–¥πΑΗΓΨΧβΡΩΓΩ‘Ύ“ΜΗω≤ΜΆΗΟςΒΡΚ–Ή”άοΉΑ”–÷Μ”–―’…Ϊ≤ΜΆ§ΒΡΚΎΓΔΑΉΝΫ÷÷«ρΙ≤40ΗωΘ§–ΓάνΉωΟΰ«ρ ‘―ιΘ§ΥΐΫΪΚ–Ή”άοΟφΒΡ«ρΫΝ‘»Κσ¥”÷–ΥφΜζΟΰ≥ω“ΜΗω«ρΦ«œ¬―’…ΪΘ§‘ΌΑ―ΥϋΖ≈ΜΊΚ–Ή”÷–Θ§≤ΜΕœ÷ΊΗ¥…œ ωΙΐ≥ΧΘ§œ¬±μ « ‘―ι÷–ΒΡ“ΜΉιΆ≥ΦΤ ΐΨίΘΚ
Οΰ«ρΒΡ¥Έ ΐn | 100 | 200 | 300 | 500 | 800 | 1000 | 3000 |
ΟΰΒΫΑΉ«ρΒΡ¥Έ ΐm | 63 | 124 | 178 | 302 | 488 | 600 | 1800 |
ΟΰΒΫΑΉ«ρΒΡΤΒ¬ | 0.63 | 0.62 | 0.593 | 0.604 | 0.61 | ΓΓ ΓΓ | ΓΓ ΓΓ |
Θ®1Θ©Άξ≥……œ±μΘΜ
Θ®2Θ©»τ¥”Κ–Ή”÷–ΥφΜζΟΰ≥ω“ΜΗω«ρΘ§‘ρΟΰΒΫΑΉ«ρΒΡΗ≈¬ PΘΫΓΓ ΓΓΘΜΘ®ΫαΙϊ±ΘΝτ–Γ ΐΒψΚσ“ΜΈΜΘ©
Θ®3Θ©ΙάΥψ’βΗω≤ΜΆΗΟςΒΡΚ–Ή”άοΑΉ«ρ”–Εύ…ΌΗωΘΩ