题目内容
【题目】如图,在平面直角坐标系中,点A(n,m)在第一象限,AB⊥x轴于B,AC⊥y轴于C,(m﹣3)2+n2﹣6n+9=0,过C点作∠ECF分别交线段AB、OB于E、F两点. 
(1)求m、n的值并写出A、B、C三点的坐标;
(2)若OF+BE=AB,求证:CF=CE.
【答案】
(1)解:将(m﹣3)2+n2=6n﹣9变形得:(m﹣3)2+(n﹣3)2=0,
∴m=3,n=3,
∴A(3,3),B(3,0),C(0,3)
(2)解:∵OF+BE=AB,AE+EB=AB,
∴AE=OF,
∵四边形ABCD为正方形,
∴AC=OC,∠A=∠COF=90°,
在△ACE和△OCF中,
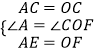 ,
,
∴△ACE≌△OCF(SAS),
∴CF=CE;
【解析】(1)已知等式变形后,利用非负数的性质求出m与n的值,即可确定出A,B,C的坐标;(2)由AE+EB=AB,以及OF+BE=AB,得到AE=OF,根据四边形ABOC为正方形,得到CA=CO,且∠A=∠COF=90°,利用SAS得到三角形ACE与三角形OCF全等,利用全等三角形对应边相等得到CF=CE;

练习册系列答案
相关题目