题目内容
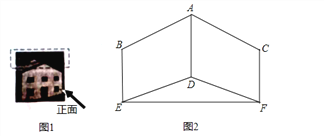
【题目】如图,图1是某仓库的实物图片,图2是该仓库屋顶(虚线部分)的正面示意图,BE、CF关于AD轴对称,且AD、BE、CF都与EF垂直,AD=3米,在B点测得A点的仰角为30°,在E点测得D点的仰角为20°,EF=6米,求BE的长.(结果精确到0.1米,参考数据:sin20°≈0.34,cos20°≈0.94,tan20°≈0.36,![]() ≈1.73)
≈1.73)
【答案】BE的长约为2.4米.
【解析】延长AD交EF于点M,过B作BN⊥AD于点N,可证四边形BEMN为矩形,分别在Rt△ABN和Rt△DEM中求出AN、DM的长度,即可求得BE=MN=AD-AN+DM的长度.
解:延长AD交EF于点M,过B作BN⊥AD于点N,
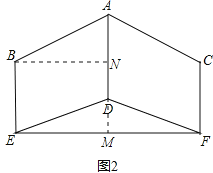
∵BE、CF关于AD轴对称,且AD、BE、CF都与EF垂直,
∴四边形BEMN为矩形,EM=MF=![]() EF=3米,
EF=3米,
∴BN=EM=3米,BE=MN,
在Rt△ABN中,
∵∠ABN=30°,BN=3米,![]() =tan30°,
=tan30°,
∴AN=BNtan30°=3×![]() =
=![]() (米),
(米),
在Rt△DEM中,
∵∠DEM=20°,EM=3米,![]() =tan20°,
=tan20°,
∴DM=EMtan20°≈3×0.36=1.08(米),
∴BE=MN=(AD-AN)+DM=3-![]() +1.08≈3-1.73+1.08=2.35≈2.4(米).
+1.08≈3-1.73+1.08=2.35≈2.4(米).
答:BE的长度为2.4米.
“点睛”本题考查了解直角三角形的应用,解答本题的关键是根据仰角和俯角的知识构造直角三角形,运用解直角三角形的知识分别求出AN、DM的长度,难度适中.

练习册系列答案
 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案 英才计划同步课时高效训练系列答案
英才计划同步课时高效训练系列答案
相关题目


