题目内容
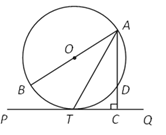
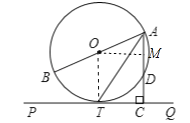
【题目】如图，
为⊙O的直径， D、T是圆上的两点，且AT平分∠BAD，过点T作AD延长线的垂线PQ，垂足为C．
（1）求证：PQ是⊙O的切线；
（2）若⊙O的半径为2，
，求弦AD的长.
【答案】(1)见解析;(2)2.
【解析】分析：（1）连接OT，只要证明OT⊥PC即可解决问题；
（2）作OM⊥AC，易知OM=TC=
，OA=2．在Rt△OAM中，求出AM即可解决问题；
详解：（1）连接OT．
∵OT=OA，∴∠ATO=∠OAT．
又∠TAC=∠BAT，∴∠ATO=∠TAC，∴OT∥AC．
∵AC⊥PQ，∴OT⊥PQ，∴PQ是⊙O的切线．
（2）过点O作OM⊥AC于M，则AM=MD．
又∠OTC=∠ACT=∠OMC=90°，
∴四边形OTCM为矩形，∴OM=TC=．
在Rt△AOM中，AM═
=1，
∴弦AD的长为2．
练习册系列答案
相关题目
【题目】为了了解同学们每月零花钱的数额，校园小记者随机调查了本校部分同学，根据调查结果，绘制出了如下两个尚不完整的统计图表．
调查结果统计表
组别 | 分组（单位：元） | 人数 |
A | 0≤x＜30 | 4 |
B | 30≤x＜60 | 16 |
C | 60≤x＜90 | a |
D | 90≤x＜120 | b |
E | x≥120 | 2 |
请根据以上图表，解答下列问题：
（1）填空：这次被调查的同学共有__人，a+b=__，m=___；
（2）求扇形统计图中扇形C的圆心角度数；
（3）该校共有学生1000人，请估计每月零花钱的数额x在60≤x＜120范围的人数．
