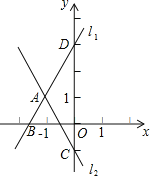题目内容
【题目】如图,在平面直角坐示系xOy中,直线![]() 与直线
与直线![]() 交于点A(3,m).
交于点A(3,m).

(1)求k,m的値;
(2)己知点P(n,n),过点P作垂直于y轴的直线与直线![]() 交于点M,过点P作垂直于x轴的直线与直线
交于点M,过点P作垂直于x轴的直线与直线![]() 交于点N(P与N不重合).若PN≤2PM,结合图象,求n的取值范围.
交于点N(P与N不重合).若PN≤2PM,结合图象,求n的取值范围.
【答案】(1) k=-2;(2) n的取值范围为:![]() 或
或![]()
【解析】
(1)把A点坐标代入y=x-2中,求得m的值,再把求得的A点坐标代入y=kx+7中,求得k的值;
(2)根据题意,用n的代数式表示出M、N点的坐标,再求得PM、PN的值,根据PN≤2PM,列出n的不等式,再求得结果.
(1)∵直线y=kx+7与直线y=x-2交于点A(3,m),
∴m=3k+3,m=1.
∴k=-2.
(2)∵点P(n,n),过点P作垂宜于y轴的直线与直线y=x-2交于点M,
∴M(n+2,n).
∴PM=2.
∴PN≤2PM,
∴PN≤4.
∵过点P作垂直于x轴的直线与直线y=kx+7交于点N,k=-2,
∴N(n,-2n+7).
∴PN=|3n-7|.
当PN=4时,如图,即|3n-7|=4,
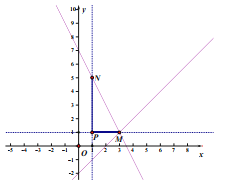
∴n=l或n=![]()
∵P与N不重合,
∴|3n-7|![]() 0.
0.
∴![]()
当PN≤4(即PN≤2PM)吋,
n的取值范围为:![]() 或
或![]()

练习册系列答案
相关题目