题目内容
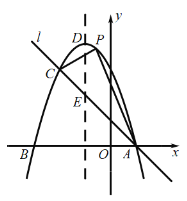
【题目】如图，抛物线
与
轴交于点
，顶点坐标
，与
轴的交点在
，
之间（包含端点），则下列结论：①
；②
；③对于任意实数
，
总成立；④关于的方程
有两个不相等的实数根．其中结论正确的个数为（ ）
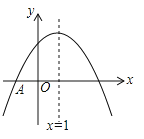
A.
个B.
个C.
个D.
个
【答案】C
【解析】
根据抛物线图像的性质得到a的范围，根据对称轴和x轴上的点可得到两个等量关系，变形替换从而可以得到①②正确，根据顶点最高可得到③正确，由数形结合可得到④错误．
∵抛物线的开口向下
∴a<0
∵对称轴x=
=1
∴b=2a
∴3a+b=a
∴3a+b<0，故①正确；
∵ A(1,0)在抛物线上
∴ab+c=0
∴3a +c=0
∴c=3a
∵c在2,3之间
∴2≤3a≤3
∴1≤a≤
，故②正确；
∵顶点坐标
，且当x=1时，y有最大值，最大值为n
∴对于任意实数m，a+b+c≥am
+bm+c
∴a+b≥am+bm ，故③正确
∵顶点坐标
∴y=ax+bx+c与y=n只有一个交点
∴y=ax+bx+c与y=n+1没有交点，故④错误
故选C
练习册系列答案
课堂全解字词句段篇章系列答案
步步高口算题卡系列答案
相关题目
