题目内容
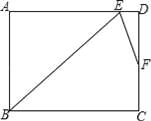
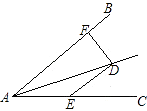
【题目】已知:如图,∠BAC的角平分线与BC的垂直平分线DG交于点D,DE⊥AB,DF⊥AC,垂足分别为E,F.
①求证:BE=CF;
②若AF=5,BC=6,求△ABC的周长.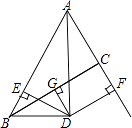
【答案】证明:①连结CD, 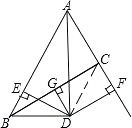
∵D在BC的中垂线上
∴BD=CD
∵DE⊥AB,DF⊥AC
AD平分∠BAC
∴DE=DF
∠BED=∠DCF=90°
在RT△BDE和RT△CDF中,![]() ,
,
∴RT△BDE≌RT△CDF(HL),
∴BE=CF;
②解:由(HL)可得,Rt△ADE≌Rt△ADF,
∴AE=AF=5,
∴△ABC的周长=AB+BC+AC,
=(AE+BE)+BC+(AF﹣CF)
=5+6+5
=16.
【解析】①连接CD,根据垂直平分线性质可得BD=CD,可证RT△BDE≌RT△CDF,可得BE=CF;②根据Rt△ADE≌Rt△ADF得出AE=AF解答即可.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目