题目内容
【题目】如图，点
分别是边长为2的正六边形中不相邻三条边的中点，则
的周长为（ ）
A.6B.
C.
D.9
【答案】D
【解析】
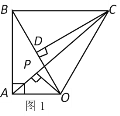
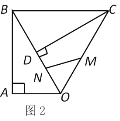
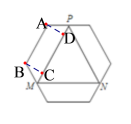
由题意得∠ABM=120°，AB∥MP，从而得∠BMC=∠APD=60°，作AD⊥PM于点D，作BC⊥PM于点C，得四边形ABCD是矩形，进而得PM=CD+ MC+PD=3，即可求解．
∵点
分别是边长为2的正六边形中不相邻三条边的中点，
∴∠ABM=120°，AB∥MP，
∴∠BMC=∠APD=60°，
作AD⊥PM于点D，作BC⊥PM于点C，
∴MC=PD=
BM=
AB=×2=，BC∥AD，
∴四边形ABCD是平行四边形，
又∵∠BCD=90°，
∴四边形ABCD是矩形，
∴CD=AB，
∴PM=CD+ MC+PD=2++=3，
∴
的周长为：9．
故选D．
练习册系列答案
阅读快车系列答案
相关题目
