题目内容
【题目】如图,矩形ABCD的对角线相交于点O,AE平分∠BAD交BC于E, 若∠CAE=15°则∠BOE=( )

A. 30° B. 45° C. 60° D. 75°
【答案】D
【解析】
∵矩形ABCD,
∴AD∥BC,AC=BD,OA=OC,OB=OD,∠BAD=90°,
∴OA=OB,∠DAE=∠AEB,
∵AE平分∠BAD,
∴∠BAE=∠DAE=45°=∠AEB,
∴AB=BE,
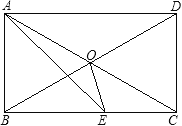
∵∠CAE=15°,
∴∠DAC=45°-15°=30°,
∠BAC=60°,
∴△BAO是等边三角形,
∴AB=OB,∠ABO=60°,
∴∠OBC=90°-60°=30°,
∵AB=OB=BE,
∴∠BOE=∠BEO=![]() (180°-30°)=75°.
(180°-30°)=75°.
故选D.
本题主要考查了三角形的内角和定理,矩形的性质,等边三角形的性质和判定,平行线的性质,角平分线的性质,等腰三角形的判定等知识点,解此题的关键是求出∠OBC的度数和求OB=BE

练习册系列答案
 培优三好生系列答案
培优三好生系列答案 优化作业上海科技文献出版社系列答案
优化作业上海科技文献出版社系列答案
相关题目






