题目内容
【题目】《九章算术》中记载了这样一道题:“今有圆材,埋在壁中,不知大小,以锯锯之,深一寸,锯道长一尺,问径几何?”用现代的语言表述为:“如果AB为⊙O的直径,弦CD⊥AB于E,AE=1寸,CD=10寸,那么直径AB的长为多少寸?”请你补全示意图,并求出AB的长.
【答案】解:如图所示,连接OD.
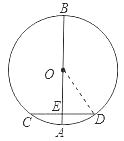
∵弦CD⊥AB,AB为圆O的直径,
∴E为CD的中点,
又∵CD=10寸,
∴CE=DE= ![]() CD=5寸,
CD=5寸,
设OD=OA=x寸,则AB=2x寸,OE=(x﹣1)寸,
由勾股定理得:OE2+DE2=OD2,
即(x﹣1)2+52=x2,
解得:x=13,
∴AB=26寸,
即直径AB的长为13寸.
【解析】先根据题意画出图形,先由垂径定理求出DE的长,再在Rt△ODE中,根据勾股定理求出圆的半径,即可得出愿得 直径长。
【考点精析】关于本题考查的勾股定理的概念和垂径定理,需要了解直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2;垂径定理:平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧才能得出正确答案.

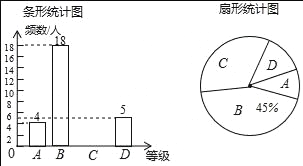
【题目】2018年10月17日是我国第五个“扶贫日”,某校学生会干部对学生倡导的“扶贫”自愿捐款活动进行抽样调查,得到一组学生捐款情况的数据,对学校部分捐款人数进行调查和分组统计后,将数据整理成如图所示的统计图,(图中信息不完整),已知A.B两组捐款人数的比为1:5.

被调查的捐款人数分组统计表:
组别 | 捐款额x/元 | 人数 |
A | 1≤x<10 | a |
B | 10≤x<20 | 100 |
C | 20≤x<30 | ______ |
D | 30≤x<40 | ______ |
E | 40≤x | ______ |
请结合以上信息解答下列问题:
(1)求a的值和参与调查的总人数;
(2)补全“被调查的捐款人数分组统计图1”并计算扇形B的圆心角度数;
(3)已知该校有学生2200人,请估计捐款数不少于30元的学生人数有多少人?