题目内容
【题目】如图,在△ABC中,∠C=90°,点D在AB上,BC=BD,DE⊥AB交AC于点E,△ABC的周长为12,△ADE的周长为6,则BC的长为( ) 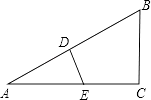
A.3
B.4
C.5
D.6
【答案】A
【解析】解:设BC=BD=x,AD=y,因为∠C=∠ADE=90°∠A=∠A,所以△ADE∽△ACB;两三角形的周长之比为1:2,所以AD:AC=1:2,则AC=2y; 根据三角形ABC的周长为12得:x+(x+y)+2y=12;即:2x+3y=12…①
根据勾股定理得:(2y)2+x2=(x+y)2 , 即:2x=3y…②
联合①②得:x=3,y=2;
故应选A.
设BC=BD=x,AD=y,△ABD和△ABC相似,根据三角形的性质相似三角形周长的比等于对应边的比进行解答.

练习册系列答案
相关题目