题目内容
已知反比例函数的解析式为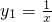
，一次函数的解析式为y2=x，且y1与y2相交两点A，B，求当y1＞y2时，x的取值范围
- A.-1＜x＜0或x＞1
- B.0＜x＜1或x＜-1
- C.0＜x＜1或x＞1
- D.-1＜x＜1
B
分析：先求出反比例函数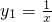与一次函数的y2=x的交点坐标，再根据它们图象的性质即可得出当y1＞y2时，x的取值范围．
解答：
解：解方程组
，解得
或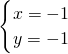
，
即反比例函数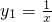与一次函数的y2=x的交点坐标为（1，1），（-1，-1）．
由图象可知，当y1＞y2时，0＜x＜1或x＜-1．
故选B．
点评：此题主要考查了反比例函数与一次函数交点坐标的性质，体现了数形结合的思想，根据图象确定自变量的取值范围，同学们应牢固掌握．
分析：先求出反比例函数
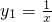与一次函数的y2=x的交点坐标，再根据它们图象的性质即可得出当y1＞y2时，x的取值范围．解答：
解：解方程组，解得或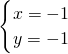，即反比例函数
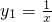与一次函数的y2=x的交点坐标为（1，1），（-1，-1）．由图象可知，当y1＞y2时，0＜x＜1或x＜-1．
故选B．
点评：此题主要考查了反比例函数与一次函数交点坐标的性质，体现了数形结合的思想，根据图象确定自变量的取值范围，同学们应牢固掌握．
练习册系列答案
名师指导一卷通系列答案
相关题目
已知反比例函数的解析式为y=
已知反比例函数的解析式为y=
（k≠1）．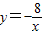
，那么当自变量x＜-4时，函数值y的取值范围是（ ）