题目内容
 已知反比例函数的解析式为y=
已知反比例函数的解析式为y=| 1-k |
| x |
(1)在反比例函数图象的每一条曲线上,y随着x的增大而增大,求k的取值范围;
(2)在(1)的条件下点A为双曲线y=
| 1-k |
| x |
分析:(1)根据反比例函数的性质得到1-k<0,然后解不等式即可;
(2)设B(t,t),双曲线解析式为y=
,利用AB∥x轴且A点在反比例函数图象上可得到A点坐标为(
,t),然后利用勾股定理分别表示出AB2=(t-
)2,OA2=(
)2+t2,再利用AB2-OA2=4,得到方程(t-
)2-[(
)2+t2]=4,再解方程即可得到m的值,从而可确定反比例函数的解析式.
(2)设B(t,t),双曲线解析式为y=
| m |
| x |
| m |
| t |
| m |
| t |
| m |
| t |
| m |
| t |
| m |
| t |
解答: 解:(1)∵在双曲线的每个分支内,y随着x的增大而增大,
解:(1)∵在双曲线的每个分支内,y随着x的增大而增大,
∴1-k<0,
∴k>1;
(2)点B在直线y=x上,设B(t,t),1-k=m(m≠0),
故双曲线解析式为y=
(m≠0),
∵AB∥x轴,
∴A点的纵坐标为t,
把y=t代入y=
得x=
,
∴A点坐标为(
,t),
∴AB2=(t-
)2,OA2=(
)2+t2,
∵AB2-OA2=4,
∴(t-
)2-[(
)2+t2]=4,解得:m=-2,
故1-k=-2,
∴反比例函数的解析式为y=
.
 解:(1)∵在双曲线的每个分支内,y随着x的增大而增大,
解:(1)∵在双曲线的每个分支内,y随着x的增大而增大,∴1-k<0,
∴k>1;
(2)点B在直线y=x上,设B(t,t),1-k=m(m≠0),
故双曲线解析式为y=
| m |
| x |
∵AB∥x轴,
∴A点的纵坐标为t,
把y=t代入y=
| m |
| x |
| m |
| t |
∴A点坐标为(
| m |
| t |
∴AB2=(t-
| m |
| t |
| m |
| t |
∵AB2-OA2=4,
∴(t-
| m |
| t |
| m |
| t |
故1-k=-2,
∴反比例函数的解析式为y=
| -2 |
| x |
点评:题考查了反比例函数的综合题:反比例函数y=
(k≠0)的图象为双曲线,当k<0,图象发布在第二、四象限,在双曲线的每个分支内,y随着x的增大而增大;掌握待定系数法求反比例函数解析式;运用勾股定理计算线段的长度.
| k |
| x |

练习册系列答案
 考前必练系列答案
考前必练系列答案
相关题目
 已知反比例函数的解析式为y=
已知反比例函数的解析式为y= (k≠1).
(k≠1).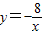 ,那么当自变量x<-4时,函数值y的取值范围是( )
,那么当自变量x<-4时,函数值y的取值范围是( )